시계열 데이터 분석 절차(3/6) - 시계열 데이터 전처리(1)
◈ '시계열 데이터 분석 절차' 목차 ◈
1. 시계열 데이터 분석 절차(1/6) - 시계열 데이터 패턴 추출
2. 시계열 데이터 분석 절차(2/6) - 시계열 데이터 분리
3. 시계열 데이터 분석 절차(3/6) - 시계열 데이터 전처리(1)
시계열 데이터 내 X요인들간의 관계를 파악하고 X요인에 대한 데이터 전처리 방법을 살펴보자
4. 시계열 데이터 분석 절차(4/6) - 시계열 데이터 전처리(2)
5. 시계열 데이터 분석 절차(5/6) - 시계열 레퍼런스 모델 구현 및 성능 확인
6. 시계열 데이터 분석 절차(6/6) - 분석 종료 위한 잔차 진단
시계열 예측 정확성을 높일 수 있도록 현실적인 데이터 패턴을 반영하여 X요인과 Y요인에 대해 데이터 전처리를 진행해야 한다.
X요인에 필요한 데이터 전처리는 스케일 조정과 다중 공선성 제거 등이 있다.
이는 시계열 데이터여서 하는 과정이라기 보다 시계열 데이터 바탕으로 회귀 예측 모델을 만들 경우 필요한 내용이다. (다시 말해 시계열 데이터가 아닌 일반 데이터의 회귀 예측 모델 생성 시에도 같은 전처리를 고려해야 한다.)
1. 변수 간 스케일 조정
■ Standard Scaler

. sklearn.preprocessing.StandarScaler()
. 각 변수(Feature)가 정규분포를 따른다는 가정이기에 정규분포가 아닐 시 최선이 아닐 수 있음
■ Min-Max Scaler
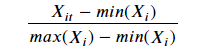
. sklearn.preprocessing.MinMaxScaler()
. 가장 많이 활용되는 알고리즘으로 최소 ~ 최대 값이 0~1 또는 -1 ~ 1 사이의 값으로 변환
. 각 변수(Feature)가 정규분포가 아니거나 표준 편차가 매우 작을 때 효과적
■ Robust Scaler
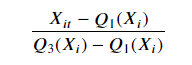
. sklearn.preprocessing.RobustScaler()
. 최소-최대 스케일러와 유사하지만 최소, 최대 대신에 IQR (Interquartile Range) 중 25% 와 75%값을 사용하여 변환
. 이상치(Outlier)에 영향을 최소화하였기에 이상치가 있는 데이터에 효과적이고 적은 데이터에도 효과적인 편임
■ Normalizer

. sklearn.preprocessing.Normalizer()
. 각 변수(Feature)를 전체 n개 모든 변수들의 크기들로 나누어서 변환
. 각 변수들의 값을 원점으로부터 반지름 1만큼 떨어진 범위내로 변환

### Functionalize
### scaling of X_train and X_test by X_train_scaler
def feature_engineering_scaling(scaler, X_train, X_test):
# preprocessing.MinMaxScaler()
# preprocessing.StandardScaler()
# preprocessing.RobustScaler()
# preprocessing.Normalizer()
scaler = scaler
scaler_fit = scaler.fit(X_train)
X_train_scaling = pd.DataFrame(scaler_fit.transform(X_train),
index=X_train.index, columns=X_train.columns)
X_test_scaling = pd.DataFrame(scaler_fit.transform(X_test),
index=X_test.index, columns=X_test.columns)
return X_train_scaling, X_test_scaling
# X_train_feRS, X_test_feRS = feature_engineering_scaling(preprocessing.Normalizer(), X_train_feR, X_test_feR)
2. 다중 공선성
2.1 X와 Y 관계성 시각화
종속 변수 Y와 독립 변수 X1, X2, X3, ... 간의 관계를 통한 시계열 회귀 분석을 하기 앞서,
X가 Y를 예측하는 데 도움이 되는 지 시각적으로 확인할 필요가 있다.
사실 현업에서는 X와 Y 간의 관계보다 X요인들간의 관계가 더 깊은 경우가 많다. 이렇게 X요인들간의 관계가 깊은 경우, 아무리 Feature Engineering 을 통해 X 요인을 생성하고 새로운 알고리즘을 적용한다 해도 결과는 크게 유의미하지 않게 된다.그래서 더더욱 분석 모델을 구현하기 앞서 X가 Y에 얼마나 영향을 미치는 지 시각적으로 확인할 필요가 있다.
■ Histogram
Y의 Histogram 과 비슷한 Histogram 모양을 갖는 요인 X는 Y와의 연관성이 높다고 볼 수 있다.
raw_fe.hist(bins=20, grid=True, figsize=(16,12))
plt.show()
■ Box-plot
요인 X에 따라 그룹을 구분하여 그룹 간의 Box-plot 을 비교할 때, 그룹 간의 Y값 데이터 분포가 다르다면 해당 요인 X는 Y와의 연관성이 높다고 볼 수 있다.
#계절성에 따른 y값의 box-plot
raw_fe.boxplot(columns='count', by='season', grid=True, figsize=(12,5))
plt.ylim(0,1000)
#휴일여부에 따른 y값의 box-plot
raw_fe.boxplot(columns='count', by='holiday', grid=True, figsize=(12,5))
plt.ylim(0,1000)
■ Scatter plot
요인 X에 따라 그룹을 구분하여 그룹 간의 Scatter plot 을 비교할 때, 그룹 간의 Y값 데이터 분포가 다르다면 해당 요인 X는 Y와의 연관성이 높다고 볼 수 있다.
#휴일 여부에 따라 시간 별 y값에 대한 scatter plot
raw_fe[raw_fe.holiday==0].plot.scatter(y='count', x='Hour', grid=True, figsize=(12,5))
plt.show()
raw_fe[raw_fe.holiday==1].plot.scatter(y='count', x='Hour', grid=True, figsize=(12,5))
plt.show()
#3차원적인 scatter plot
raw_fe[raw_fe.holiday==0].plot.scatter(y='count', x='Hour', c='temp', grid=True, figsize=(12,5))
■ crosstab
pd.crosstab(index=raw_fe['count'], columns=raw_fe['weather'], margins=True)
#margins 옵션은 총 합계에 대한 표시 여부
■ scatter_matrix
모든 변수 X, Y 간의 상관성을 시각화한다. 변수 간의 상관성이 높을수록 직선의 형태를 띈다.
pd.plotting.scatter_matrix(raw_fe, figsize=(18,18), diagonal='kde')
■ correlation
모든 변수간의 상관 계수를 수치 및 시각적으로 나타내어, X들간의 관계가 높은 지 X와 Y간의 관계가 높은 지 확인해야 한다.Y와 관계성이 많은 변수가 많을 수록 좋다.
#모든 변수간의 상관 계수를 나타낸 표 생성
corr = raw_fe.corr()
#상관 계수에 대해 시각화 (상관 계수가 클수록 색을 진하게 표현)
corr.style.background_gradient(cmap='coolwarm').set_precision(2).set_properties(**{'font-size':'15pt'})
#set_precision(2) : 상관 계수를 소수점 2째자리까지 표현
#set_properties(**{'font-size':'15pt')}) : 폰트 사이즈를 15로 설정
2.2 다중공선성 제거
다중공선성(Multicollinearity)은 다음과 같은 경우 발생한다.
˙ 독립변수의 일부가 다른 독립변수의 조합으로 표현될 수 있는 경우 ex. X1= aX2+bX3
˙ 독립변수들이 서로 독립이 아니라 상호 상관 관계가 강한 경우
˙ 독립변수의 공분산 행렬(Covariance Matrix) 벡터공간(Vector Space)의 차원과 독립변수의 차원이 같지 않은 경우
다중공선성을 확인하고 제거하는 방법은 크게 두 가지가 있다.
■ Variance Inflation Factor(VIF)

VIF는 독립변수를 다른 독립변수로 선형회귀한 성능을 의미하며, 이를 통해 상호 가장 의존적인 독립변수를 제거할 수 있다.
의존성이 낮은(분산이 작은) 독립변수들을 선택하거나 의존성이 높은 독립변수들을 제거할 수 있다.

■ Principal Component Analysis(PCA)