My Data Story
[딥러닝] 인공 신경망 - 다층 퍼셉트론 본문
◈ '인공 신경망' 목차 ◈
2. 다층 퍼셉트론
다층 퍼셉트론의 구조와 활성화 함수에 대해 살펴보고, 이를 활용한 회귀 및 분류 모델을 살펴보자.
1. 다층 퍼셉트론 구조
다층 퍼셉트론은 입력층 하나와 은닉층이라 불리는 하나 이상의 TLU 층과 마지막 출력층으로 구성된다.

이때 은닉층을 여러 개 쌓아 올린 인공 신경망을 심층 신경망 Deep Neural Network (DNN) 이라고 한다.
2. 다층 퍼셉트론 훈련
2.1 역전파 훈련 알고리즘
다층 퍼셉트론 훈련하기 위해 역전파 훈련 알고리즘을 사용한다.
간단히 말해, 이 알고리즘은 효율적인 기법으로 그레이디언트를 자동으로 계산하는 경사 하강법이다.
역전파 알고리즘은 네트워크를 두 번(정방향과 역방향) 통과하여 모든 모델 파라미터에 대한 네트워크 오차의 그레이디언트를 계산할 수 있다. 다른 말로 하면 오차를 감소시키기 위해 각 연결 가중치와 편향값이 어떻게 바뀌어야 하는 지 알 수 있다.
그레이디언트를 구하고 나면 평범한 경사 하강법을 수행한다.
cf. 자동 미분
자동으로 그레이디언트를 계산하는 것을 자동 미분이라 부른다.
각기 장단점을 가진 여러 가지 자동 미분 기법이 있는데, 역전파에서 사용하는 기법은 후진 모드 자동 미분이다.
이 기법은 빠르고 정확하며 미분할 함수가 변수(ex. 연결 가중치)가 많고 출력이 적은 경우 잘 맞는다.
역전파 훈련 알고리즘 과정을 살펴보면 다음과 같다.
step1. 준비
* 미니 배치 단위
한 번에 하나의 미니 배치씩 진행하여 전체 훈련 세트를 처리한다.
* 가중치 초기화
은닉층의 연결 가중치를 랜덤하게 초기화하는 것이 중요하다.
모든 가중치와 편향을 0으로 초기화하면 층의 모든 뉴럭이 완전히 같아지고, 역전파도 뉴런을 동일하게 바꾸어 모든 뉴런이 똑같은 채로 남는다. 결국 층에 뉴런이 수 백개 있더라도 모델은 마치 뉴런이 하나인 것처럼 작동할 것이다.
반면 가중치를 랜덤하게 초기화하면 대칭성이 깨지므로 역전파가 전체 뉴런을 다양하게 훈련시킬 수 있다.
step2. 정방향 계산
각 미니 배치는 네트워크의 입력층으로 전달되어 첫 번째 은닉층으로 보내진다.
마지막 층인 출력층의 출력을 계산할 때까지 계속된다.
역방향 계산을 위해 중간 계산값을 모두 저장하는 것 외에는 예측을 만드는 것과 동일하다.
step3. 네트워크 출력 오차 측정
손실 함수를 사용하여 기대하는 출력과 네트워크의 실제 출력을 비교하여 오차를 측정한다.
step4. 역방향 계산
각 출력 연결이 이 오차에 기여하는 정도를 계산한다.
이 알고리즘은 연쇄 법칙을 사용하여, 이전 층의 연결 가중치가 이 오차의 기여 정도에 얼마나 기여했는 지 측정한다.
입력층에 도달할 때까지 역방향으로 계속된다.
오차 그레이디언트를 역방향으로 전파함으로써 네트워크에 있는 모든 연결 가중치에 대한 오차 가중치를 효율적으로 측정한다.
step5. 연결 가중치 업데이트
경사 하강법을 수행하여 계산한 오차 그레이디언트를 사용해 네트워크에 있는 모든 연결 가중치를 수정한다.
2.2 역전파 알고리즘의 활성화 함수
근본적으로 다층 퍼셉트론에서 활성화 함수는 왜 필요한 것일까?
선형 변환을 여러 개 연결해도 결국 선형 관계이기 때문이다.
즉 층 사이에 비선형성을 추가하지 않으면 아무리 층을 많이 쌓아도 하나의 층과 동일해진다.
이런 다층 퍼셉트론 모델로는 XOR 문제와 같은 문제 뿐만 아니라 복잡한 문제를 풀 수 없다.
반대로 비선형 활성화 함수가 있는 충분히 큰 심층 신경망은 이론적으로 어떤 연속 함수도 근사할 수 있게 된다.
˙로지스틱 함수 (시그모이드 함수)
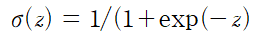
역전파 알고리즘의 활성화 함수는 계단 함수가 아닌 로지스틱(시그모이드) 함수를 사용한다.
왜냐하면 계단 함수에는 수평선 밖에 없어서 그레이디언트를 계산할 수 없기 때문이다. (미분할 수 없다.)
시그모이드 외에도 자주 사용되는 활성화 함수 몇 가지가 존재한다.
˙하이퍼볼릭 탄젠트 함수 (쌍곡 탄젠트 함수)
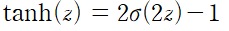
로지스틱 함수처럼 S자 모양이고 연속적이며 미분 가능하다.
출력 범위가 -1에서 1 사이다.
이 범위는 훈련 초기에 각 층의 출력을 원점 근처로 모으는 경향이 있어, 종종 빠르게 수렴되도록 도와준다.
˙ ReLU 함수

연속적이지만 z=0 에서 미분 불가능하여 기울기가 갑자기 변해서 경사 하강법이 엉뚱한 곳으로 튈 수도 있다.
z<0 이면 도함수는 0이다. 실제로 잘 작동하고 계산 속도가 빨라 기본 활성화 함수로 사용된다.
출력의 최댓값이 없어서 경사 하강법의 일부 문제를 완화해준다.

3. 회귀를 위한 다층 퍼셉트론
3.1 활성화 함수
일반적으로 회귀용 다층 퍼셉트론을 만들 때, 출력 뉴런에 활성화 함수를 사용하지 않고도 어떤 범위의 값도 출력되도록 한다.
하지만 출력이 항상 양수여야 한다면, 출력층에 ReLU 나 Softplus 활성화 함수를 사용한다.
(softplus(z) = log(1+exp(z)), z가 음수일 때 0에 가까워지고 z가 양수일 때 z에 가까워진다.)
출력이 어떤 범위 안의 값을 예측하고 싶다면 로지스틱 함수나 하이퍼볼릭 탄젠트 함수를 사용하여 레이블의 스케일을 적절한 범위로 조정할 수 있다.
3.2 손실 함수
회귀를 위한 다층 퍼셉트론의 손실 함수는 전형적으로 평균 제곱 오차이다.
훈련 세트에 이상치가 많다면 평균 절댓값 오차를 사용할 수 있다.
또는 이 둘을 조합한 후버 손실을 사용할 수 있다.
후버 손실은 오차가 임계값(기본적으로 1) 보다 작을 때 이차 함수이고, 임계값보다 크면 선형 함수이다.
선형 함수 부분은 평균 제곱 오차보다 이상치에 덜 민감하고, 이차 함수 부분은 평균 절댓값보다 더 빠르고 정확하게 수렴하게 해준다.
2.3 회귀 MLP 전형적인 구조
| 특성 | 값 |
| 하이퍼파라미터 | 일반적인 값 |
| 입력 뉴런수 | 특성마다 하나 |
| 은닉층 수 | 문제에 따라 다름. 일반적으로 1에서 5 사이 |
| 은닉층의 뉴런 수 | 문제에 따라 다름. 일반적으로 1에서 100 사이 |
| 출력 뉴런 수 | 예측 차원마다 하나씩 |
| 은닉층의 활성화 함수 | ReLU (또는 SELU) *11장참고 |
| 출력층의 활성화 함수 | 없음 (출력이 양수일 때) ReLU / softplus 사용 (출력을 특정 범위로 제한할 때) logistic/tanh 사용 |
| 손실 함수 | MES / (이상치 많으면) MAE/Huber |
4. 분류를 위한 다층 퍼셉트론
4.1 활성화 함수
다층 퍼셉트론은 분류 작업에도 사용할 수 있다.
이진 분류 문제에서는 로지스틱 활성화 함수를 가진 하나의 출력 뉴런만 필요하다.
각 샘플이 3개 이상의 클래스 중 한 클래스에만 속할 수 있다면
클래스마다 하나의 출력 뉴런이 필요하고, 출력층에는 소프트맥스 활성화 함수를 사용해야 한다.
소프트맥스 활성화 함수는 모든 예측 확률을 0과 1 사이로 만들고, 더했을 때 1이 되게 만든다. (클래스가 서로 배타적일 경우)
이를 다중 분류라 한다.

4.2 손실 함수
손실 함수로는 일반적으로 크로스 엔트로피 손실을 선택하는 것이 좋다.
4.3 분류 MLP 전형적인 구조
| 하이퍼파라미터 | 이진 분류 | 다중 레이블 분류 | 다중 분류 |
| 입력층과 은닉층 | 회귀와 동일 | 회귀와 동일 | 회귀와 동일 |
| 출력 뉴런 수 | 1개 | 레이블 마다 1개 | 클래스 마다 1개 |
| 출력층의 활성화 함수 | 로지스틱 함수 | 로지스틱 함수 | 소프트맥스 함수 |
| 손실 함수 | 크로스 엔트로피 | 크로스 엔트로피 | 크로스 엔트로피 |
'Deep Learning' 카테고리의 다른 글
| [딥러닝] 인공신경망 - 서브클래싱 API 구현 (0) | 2021.09.04 |
|---|---|
| [딥러닝] 인공 신경망 - 함수형 API 구현 (0) | 2021.09.04 |
| [딥러닝] 인공 신경망 - 시퀀셜 API 구현 (0) | 2021.09.04 |
| [딥러닝] 인공 신경망 - 케라스 API 소개 (0) | 2021.09.04 |
| [딥러닝] 인공 신경망 - 퍼셉트론 (0) | 2021.09.04 |




