My Data Story
[회귀] 선형 회귀 모델 해석 본문
◈ '회귀' 목차 ◈
5. 선형 회귀 모델 해석
회귀 모델 생성 후, 회귀 방정식에 대해 해석하며 예측 모델에 통찰을 얻을 수 있음을 살펴볼 수 있다.
1. 회귀 방정식 해석
데이터 과학에서 회귀의 가장 중요한 용도는 종속 변수를 예측하는 것이다.
하지만 때로는 예측 변수와 결과 변수간 관계의 본질을 이해하기 위해 방정식 자체로부터 통찰을 얻는 것이 중요할 때도 있다.
회귀 방정식을 검토하고 해석하는 방법에 대해 살펴보자.
1.1 예측 변수 간 상관
예측 변수 간의 상관 관계를 살펴보아야 한다.
상호 연관된 예측 변수들을 사용하면 회귀 계수의 부호와 값의 의미가 해석하기 어려울 수 있다.
상관 분석은 두 변수간의 어떤 선형적 관계를 갖고 있는 지를 분석한다.
상관 계수는 두 변수간의 연관된 정도를 나타낼 뿐 인과 관계를 나타내지 않는다.
(인과 관계는 회귀 분석을 통해 인과 관계의 방향 및 정도를 확인할 수 있다.)
상관 계수에 대해 해석하면 다음과 같다.
- 0 < 상관 계수 < 1 : 양의 상관 관계
- -1 < 상관계수 < 0 : 음의 상관 관계
- 상관계수 = 0 : 두 변수 간의 선형의 상관 관계가 없다. (아무런 관계가 없다 (X))
cf. R-Squared 값 = Coefficient-Squared 값 같다.
1.2 다중 공선성 ★
예측 변수들끼리 완벽하거나 완벽에 가까운 상관성을 갖을 때 다중공선성을 띈다고 표현한다.
극단적으로 완전 다중 공산성은 한 예측 변수가 다른 예측 변수들의 선형 결합으로 표현된다.
이러한 면에서 다중공선성은 예측 변수 사이의 중복성을 판단하는 조건이 된다.
다중 공선성은 다음과 같은 경우 발생한다.
˙ 오류로 인해 한 변수가 여러 번 포함되는 경우
˙ 요인 변수로부터 P-1 개가 아닌 P개의 가변수가 만들어진 경우
˙ 두 변수가 서로 거의 완벽하게 상관성이 있는 경우
다중 공선성을 측정하는 지표로 VIF (분산 팽창 요인) 통계량이 존재한다.
R에서 car 패키지에서 vif 통해 다중 공선성 측정할 수 있다.
보통 VIF 값이 10보다 크면 다중 공산성 관계가 있다고 할 수 있다.
그렇다면 다중 공선성이 문제인 이유가 무엇인가?
회귀 계수 추정량의 분산이 커지면서 추정한 회귀 계수의 정확성이 떨어지기 때문이다.
물론 다중 공선성이 존재하면 예측이 불완전하기는 하지만, 예측 결과에는 큰 영향이 없다.
하지만 올바른 회귀 계수 해석을 위해서 다중 공선성을 제거하는 것이 좋다.
다중 공선성을 제거하기 위해서는 다양한 방법이 존재한다.
˙ 선형 회귀 모형에 교호작용 변수 추가
˙ 상관성이 가장 높은 변수 1개만 선택 (ex. PLS, PCA - 비추)
˙ 릿지 회귀 모델 사용 (회귀 계수의 분산을 줄여줄 수 있기 때문)
˙ Tree 기반의 모델 사용
Tip!
다중 공선성은 트리, 클러스터, 최근접 이웃 알고리즘 등 회귀 유형이 아닌 방법에서는 그다지 문제가 되지 않는다.
이들 방법에서는 P-1 개 대신 P개의 가변수를 유지하는 것이 좋다.
물론 이러한 방법에서도 예측 변수의 비중복성을 유지하는 것이 여전히 미덕이다.
cf. VIF 도출 과정
1. P개의 예측 변수가 존재한다. (X1, X2, ... , Xp)
2. Xi 를 나머지 P-1 개의 예측 변수로 예측하는 선형 회귀 모델을 생성한다.
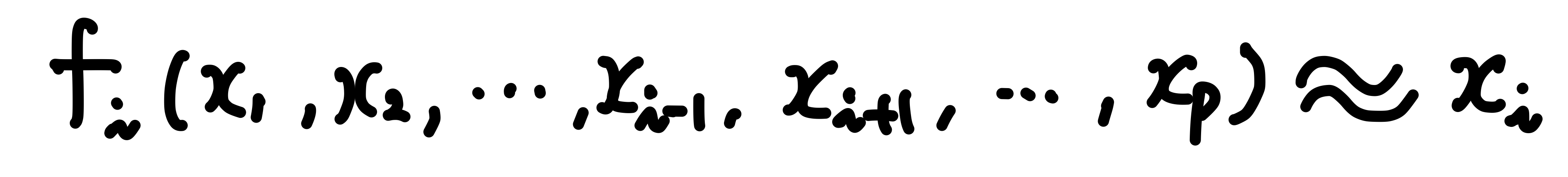
3. 생성한 선형 회귀 모델 f(i) 에 대한 R_Squared(i) 값을 계산한다.

4. VIF(i) 를 계산한다.

1.3 교란 변수
회귀 방정식에서 중요한 변수가 포함되지 못해서 생기는 누락의 문제이다.
이 경우 방정식 계수에 대한 순진한 해석은 잘못된 결론으로 이어질 수 있다.
1.4 상호 작용과 주효과
회귀 모델에 주효과(독립변수)만 사용한다면, 이는 예측 변수와 응답 변수 간의 관계가 다른 예측 변수들에 대해 독립적이라는 암묵적인 가정이 있다. 하지만 이는 종종 사실이 아니다.
예측 변수간의 강한 상호 작용이 존재할 경우, 상호 작용 항을 모델에 추가하여 구현할 수 있다.
하지만 보통 다수의 변수가 존재하는 경우, 모델에서 어떤 상호 작용을 고려해야 할 지 결정하기 매우 어렵다.
이러한 문제에 접근하는 다음과 같은 몇 가지 방법에 대해 알아보자.
˙어떤 문제에서는 사전 지식이나 직관이 이러한 상호 작용을 결정하는 데 매우 큰 도움이 된다.
˙ 단계적 선택을 활용해 다양한 모델들을 걸러낼 수 있다.
˙ 벌점을 부여하는 방식의 회귀 방법을 사용하여 자동으로 가능한 상호 작용들을 최대한 가려내도록 한다.
˙ 랜덤 포레스트나 그레이디언트 부스팅 트리 같은 트리 모델을 가장 일반적으로 사용할 수 있다.
이러한 모델들은 자동으로 최적의 상호 작용을 걸러낸다.
'Machine Learning > 2. 지도 학습 알고리즘' 카테고리의 다른 글
| [회귀] 비선형 회귀 - 다항 회귀, 스플라인 회귀 (0) | 2021.08.06 |
|---|---|
| [회귀] 선형 회귀 가설 검정 : 회귀 진단 (0) | 2021.08.06 |
| [회귀] 선형 회귀로 새로운 데이터 예측 (0) | 2021.08.06 |
| [회귀] 선형 회귀 모델 평가 및 모델 선택 (0) | 2021.08.06 |
| [회귀] 선형 회귀 모델 훈련 (0) | 2021.08.06 |




