My Data Story
[분류] 결정 트리 분류 모델 본문
◈ '결정 트리' 목차 ◈
1. 결정 트리 분류 모델
결정 트리 생성 원리와 규제 방식을 이해하고, 사이킷런에서 결정 트리 생성하는 방법에 대해 살펴보자.
트리 모델은 if-then-else 규칙의 집합체로 데이터에 숨겨진 패턴들을 발견하는 능력이 있다.
SVM 처럼 결정 트리는 분류와 회귀 작업 그리고 다중 출력 작업도 가능한 다재 다능한 머신러닝 알고리즘이다.
매우 복잡한 데이터 셋도 학습할 수 있는 강력한 알고리즘이다.
1. 결정 트리 분류 모델 생성 원리
1.1 재귀 분할
결정 트리를 만들 때는 상대적으로 같은 클래스의 데이터끼리 구분되도록 예측 변수 값을 기준으로 반복적으로 데이터를 분할한다.
이러한 과정을 재귀 분할 과정이라 한다.
응답 변수 Y와 P개의 예측 변수 집합 X(j) (j=1,2 ... , P) 있다고 가정할 때,
파티션 A를 두 개의 하위 영역으로 나누기 위한 가장 좋은 재귀적 분할 방법은 다음과 같다.
step1
모든 예측 변수 X(j)에 대해
a. X(j) 에 해당하는 모든 변수 값 s(j) 에 대해,
i. A에 해당하는 모든 레코드를 X(j) < s(j) 인 부분과 X(j) >= s(j) 인 부분으로 나눈다.
ii. A의 각 하위 분할 영역 안에 해당 클래스의 동질성을 측정한다.
cf. 분류 문제에서는 클래스의 동질성, 회귀 문제에서는 MSE 를 측정
b. 하위 분할 영역 내에서의 클래스 동질성이 가장 큰 s(j) 값을 선택한다.
모든 예측 변수 X(j) 에 대한 가능한 임계값 s(j) 의 쌍에 대해 step1 을 진행한다.
step2
클래스 동질성이 가장 큰 X(j) 와 s(j) 값을 선택하고, A를 두 부분 A1 과 A2로 나눈다.
step3
A1 과 A2 각각에 대해서 step1 ~ step2 과정을 반복한다.
이때 이전 Split 과정에서 사용되었던 예측 변수(feature) 는 또 사용될 수 있다.
그리고 Split Point 는 각 예측 변수 (feature) 축에 수직인 방향으로만 가능하다.
step4
분할해도 더 이상 분할 영역의 동질성이 개선되지 않을 정도로 충분히 분할을 진행했을 때, 알고리즘을 종료한다.
Split 이후 생성된 자식 노드 내 불순도가 0이라면 해당 노드는 더 이상 Split 진행 불가하다. 이때 노드를 리프노드라 한다.
step5
각 영역에 속한 응답 변수들의 다수결 결과에 따라 속할 클래스를 예측한다.
클래스 결과 외에 하위 분할 영역에 존재하는 클래스 별 레코드 개수에 따라 확률 값을 구할 수도 있다.
P(Y=1) = 해당 파티션 내 클래스 1에 속하는 레코드 수 / 해당 파티션 내 전체 레코드 수
이렇게 얻은 확률 P(Y=1) 통해 이진 결정을 할 수 있다. ex. P(Y=1) >= 0.5 이면 클래스 1로 할당
1.2 불순도 측정
(1) 지니 불순도
모든 샘플이 같은 클래스에 속해 있다면 순수하다고 판단하여 gini=0 이다.
지니 불순도는 노드에서 데이터가 한 클래스에 몰려 있을수록 0에 가깝다.

사이킷런에서 DecisionTreeClassifier 의 criterion 매개 변수의 기본 값은 'gini' 로 지니 불순도이다.
(2) 엔트로피 불순도
엔트로피는 분자의 무질서함을 측정하는 지표이다.
엔트로피에 대해 이해하기 위해서 정보량에 대해 이해가 필요하다.
정보량이란 어떤 사건이 가지고 있는 정보의 양으로 드물게 발생하는 사건일수록 정보량이 크다.
(일어날 확률이 적은 사건이 발생했을 때 사람들은 많이 놀란다. 따라서 정보량을 놀람의 정도로 표현하기도 한다.)
정보량은 다음과 같은 수식으로 나타낸다.
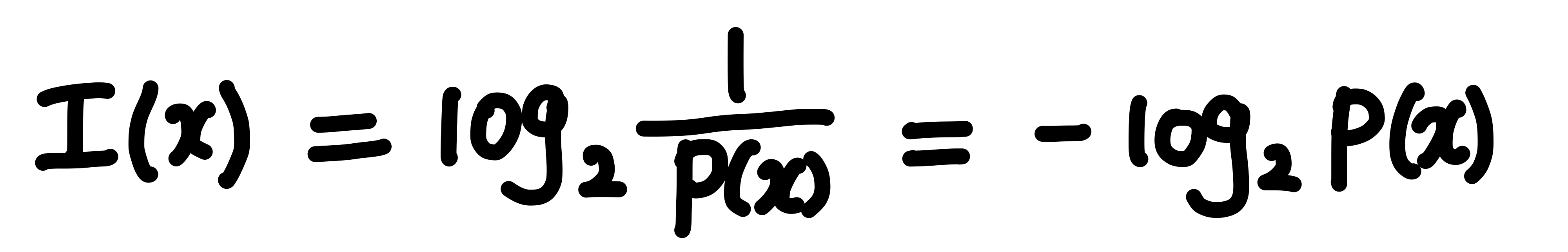
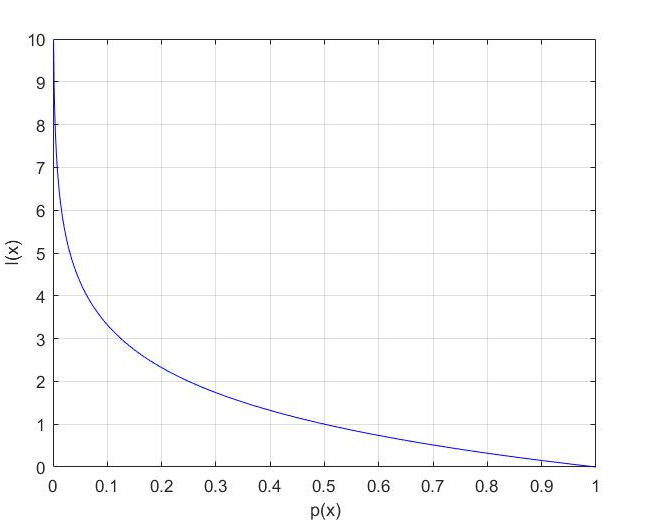
p(x) 는 사건 x가 발생할 확률로 발생 확률이 1에 가까울수록 정보량은 0에 가까움을 알 수 있다.
엔트로피는 정보량의 기댓값을 나타낸다.
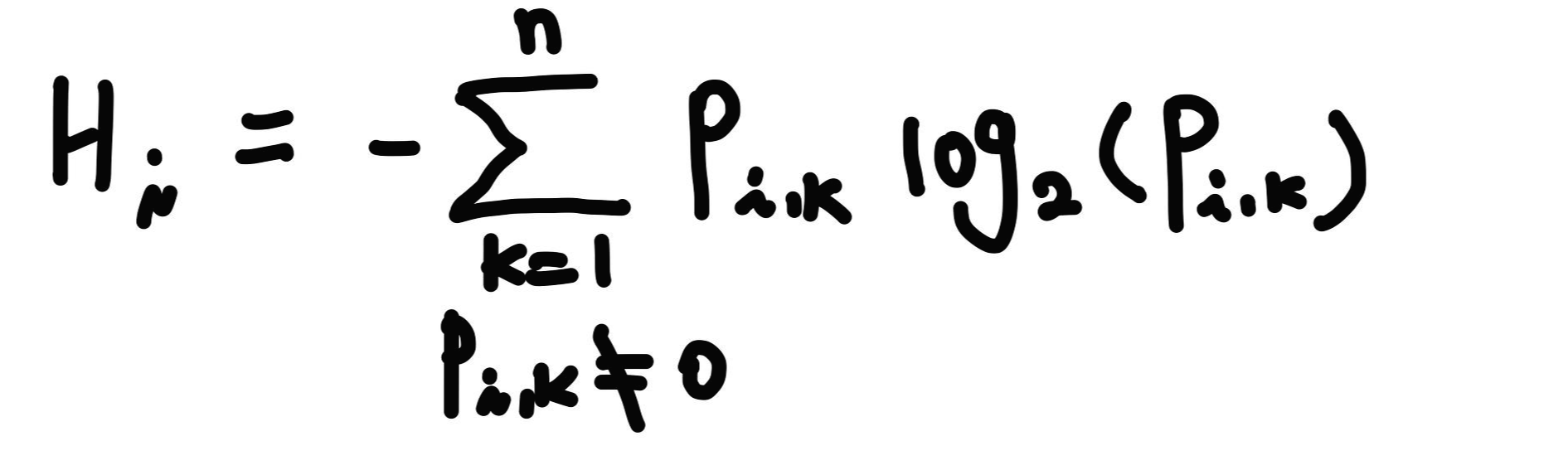
어떤 세트가 한 클래스의 샘플만 담고 있으면 엔트로피는 0이다.
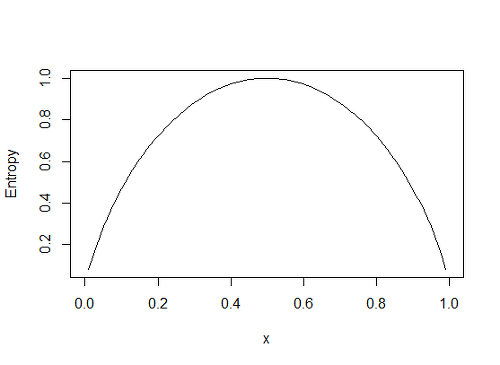
사이킷런에서 DecisionTreeClassifier 의 criterion 매개 변수 값을 'entropy' 로 지정하면 엔트로피 불순도를 사용할 수 있다.
(3) 지니 불순도와 엔트로피 중 어떤 것 사용해야 할까?
실제로 큰 차이는 없다. 둘 다 비슷한 트리를 만들어낸다.
지니 불순도가 조금 더 계산이 빨라 사이킷런의 DecisionTreeClassifier 의 기본값으로 설정하기 좋다.
그러나 다른 트리가 만들어지는 경우
지니 불순도가 가장 빈도 많은 클래스를 한 쪽 가지로 고립시키는 경향이 있는 반면,
엔트로피 불순도는 조금 더 균형 잡힌 트리를 만든다.
1.3 결정 트리 알고리즘
(1) CART 알고리즘
사이킷런은 결정 트리를 훈련시키기 위해 CART (Classification And Regression Tree) 알고리즘을 사용한다.
CART 알고리즘은 이진 트리(Binary Tree) 만을 만들어, 리프 노드를 제외한 모든 노드는 자식 노드를 두 개씩 가진다.
그리고 분류 문제 뿐 아니라 회귀 문제에도 적용 가능한 알고리즘이다.
■ 훈련 과정
step1
훈련 세트를 하나의 특성 k의 임계값 t(k) 를 사용해 두 개의 서브셋으로 나눈다. ex. 꽃잎의 길이 < 2.4cm
step2
크기에 따라 가중치가 적용된 불순도 값 기준으로 가장 순수한 서브넷으로 나눌 수 있는 (k, t(k))를 찾는다.
CART 알고리즘은 분류 문제에는 지니 불순도 지표를 사용한다.
※ 분류에 대한 CART 비용 함수

step3
max_depth (최대 깊이) 가 되면 중지하거나 불순도를 줄이는 분할을 찾을 수 없을 때 중단한다.
CART 알고리즘은 탐욕적 알고리즘 이다.
맨 위 Root 노드에서 최적의 분할을 찾으며 이어지는 자식 노드에서 같은 과정을 반복한다.
현재 단계의 분할이 몇 단계를 거쳐 가장 낮은 불순도로 이어질 수 있는 지는 고려 안 한다.
이러한 문제로 탐욕적 알고리즘은 종종 납득할 만한 솔루션이 되지만, 최적의 솔루션은 아니다.
최적 트리를 찾는 것 NP-완전 문제로 O(exp(m)) 시간이 필요하고 작은 훈련 세트에서도 어렵다.
따라서 납득할 만한 솔루션에 만족해야 한다.
그리고 모델 생성 시 한 번에 1개의 변수만을 활용하여 트리 생성하기 때문에 변수간의 Interaction 을 찾을 수 없다.
■ 계산 복잡도
예측을 하려면 결정 트리의 루트 노드부터 리프 노드까지 탐색해야 한다.
결정 트리 탐색 시,
각 노드는 하나의 특성값만 확인하기 때문에
예측에 필요한 전체 복합도는 전체 특성 수와 무관하게 O(log2(m)) 이다.
따라서 큰 훈련 세트를 다룰 때도 예측 속도가 매우 빠르다.
훈련 알고리즘 하이퍼파라미터 설정에 따른 계산 복잡도는 다음과 같다.
˙ max_featrues
훈련 알고리즘은 각 노드에서 모든 샘플의 모든 특성을 비교하는데,
max_features 설정 시, 지정된 특성 수에 한해서 비교하게 된다.
데이터 셋의 특성 개수보다 작게 설정하면 무작위로 일부 특성 선택한다.
˙ preosrt
훈련 세트가 작을 경우 (수천 개 이하의 샘플 정도) presort=True 지정하면,
미리 데이터를 정렬하여 훈련 속도를 높일 수 있다.
하지만 훈련 세트가 클 경우 훈련 속도는 더 느려진다.
(2) ID3 알고리즘
ID3 알고리즘은 엔트로피 불순도 지표를 사용하여 둘 이상의 자식 노드를 가진 결정 트리를 만든다.
트리 분기할 때, 분기 전후의 엔트로피 변화량을 나타낸 Information Gain 을 활용한다.
Information Gain 이 큰 기준으로 분기한다.
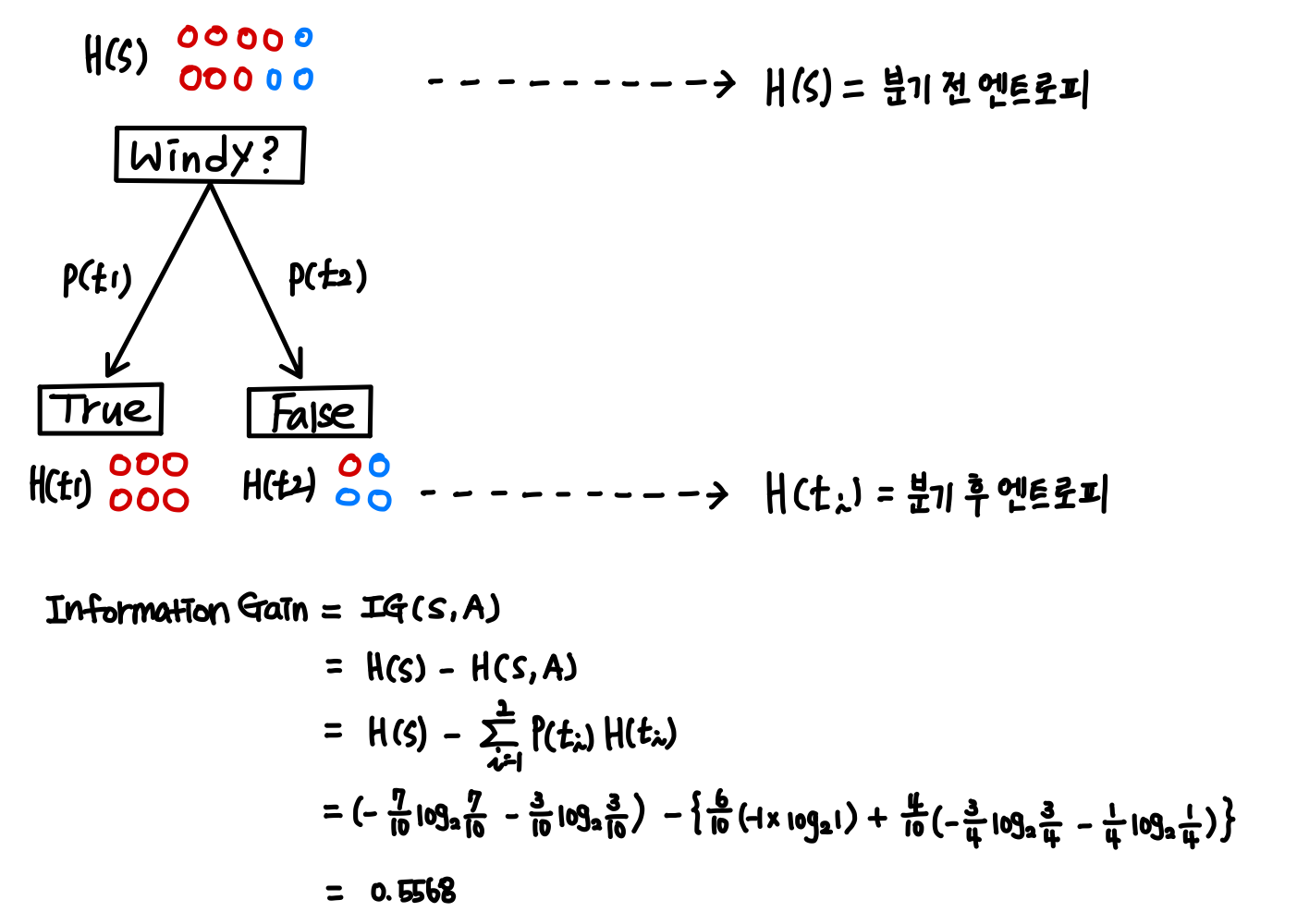
ID3 알고리즘은 명목형 데이터에만 적용 가능하고, 분류 모델에서만 적용 가능하다.
(3) C4.5 알고리즘
ID3 알고리즘을 개선하여 개발한 알고리즘이다.
C4.5 알고리즘의 개선 사항 및 특징은 다음과 같다.
▶ 연속형 데이터 적용 가능
C4.5 알고리즘은 연속형 데이터에도 적용이 가능해졌다.
연속형 데이터 분기 시 특정 break point 의 값에 대해서만 불순도를 측정한다.
그렇다면 break point 를 어떻게 지정할 것인가?
(방법1) 값이 바뀌는 모든 지점에서 측정
(방법2) Output 클래스가 바뀌는 지점에서만 측정
(방법3) Q1, median, Q3 지점에서만 측정
▶ 결측치 데이터 적용 가능
C4.5 알고리즘은 결측치가 존재해도 처리할 수 있어졌다.
step1
결측 치를 제외한 나머지 데이터에 대해 엔트로피 계산한다.
step2
Information Gain 을 Weighted Information Gain 으로 변경해 활용한다.
Weighted Information Gain = F * IG(S,A)
(F : 결측치 비율)
step3
Intrinsic Value 계산 시, 결측치들을 하나의 클래스로 간주하여 계산한다.
예를 들어, 트리 분기 시 4개의 가지가 생성된다면 결측치 클래스도 추가하여 5개의 클래스에 대한 IV를 계산한다.
▶ 정교한 불순도 지표 활용
C4.5 알고리즘도 엔트로피 불순도 지표를 사용한다.
하지만 트리 분기 시 Information Gain만 보고 판단하면 모델이 과대 적합될 수 있어
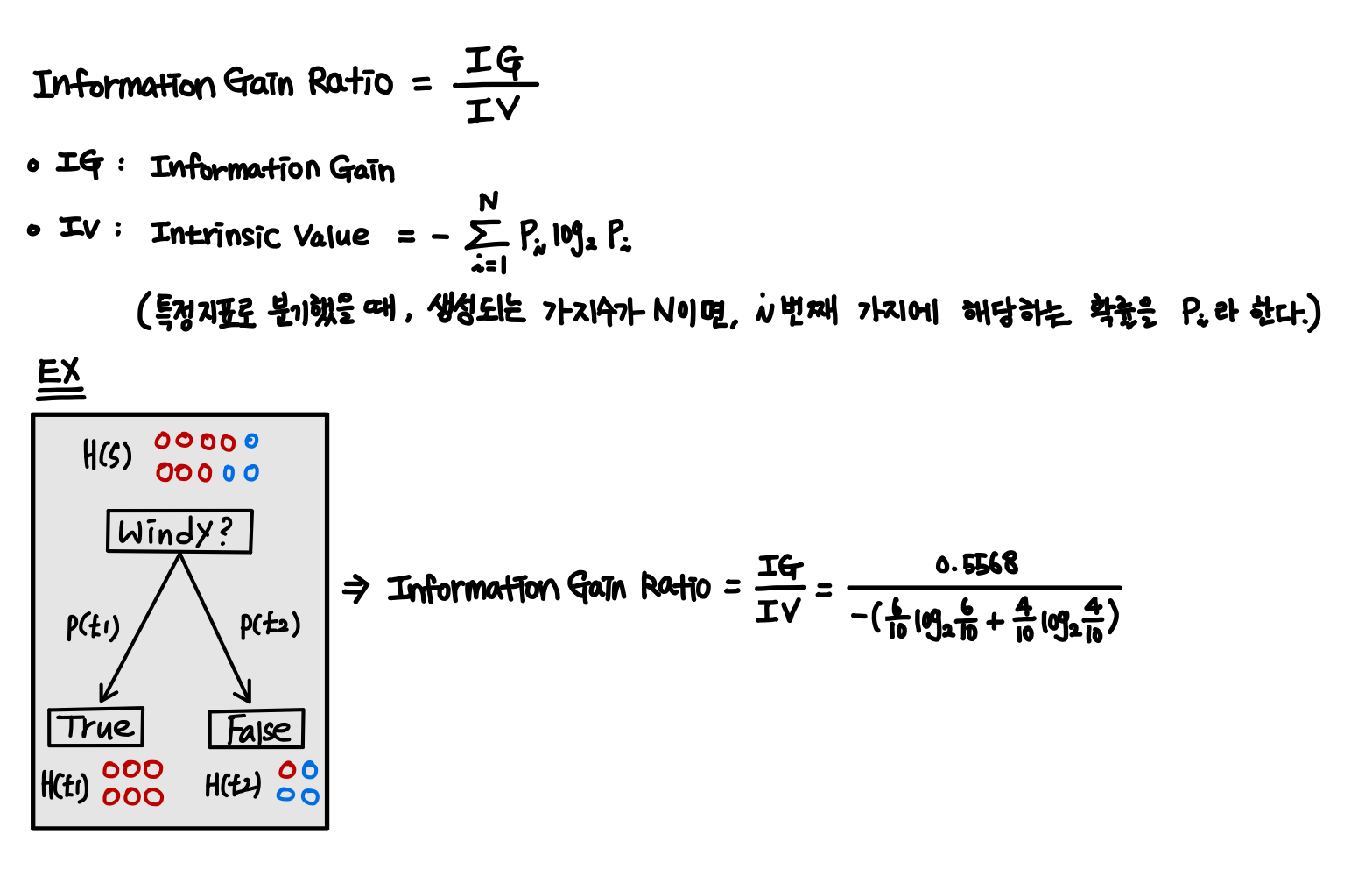
이를 보완한 정교한 불순도 지표 Information Gain Ratio 를 활용한다.
Information Gain Ratio 는 다음과 같이 계산된다.
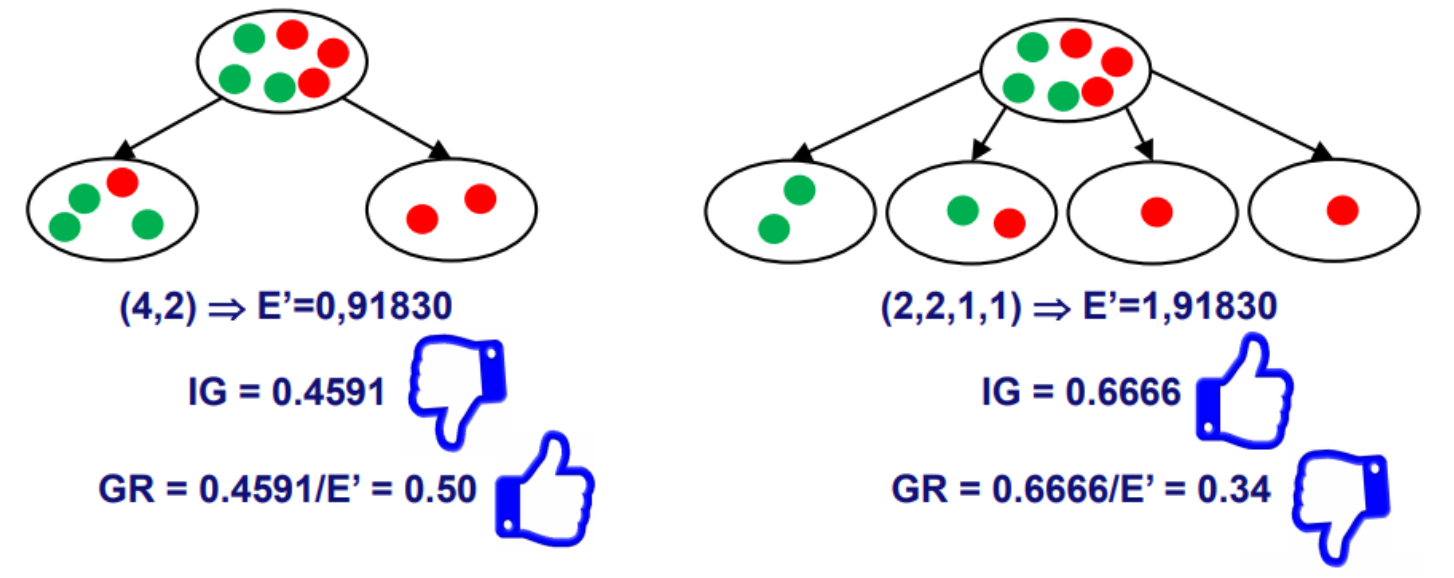
아래 그림을 살펴보면, 같은 상황에서 오른쪽 트리는 리프 노드를 여러 개 분리하여 모델이 과대 적합되었음에도 왼쪽 트리보다 더 높은 Information Gain 값을 갖는다. 하지만 Information Gain Ratio 로 판단하면 왼쪽 트리가 더 적절함을 알 수 있다.
▶ 사후 가지치기 적용
C4.5 알고리즘은 사후 가지치기 알고리즘이 적용되어,
최대한 가지 형성 후 사후 가지치기로 sub tree 의 영향도까지 고려한다.
step1
전체 데이터를 train data, prune data, test data 로 나눈다.
step2
train data 로 최대한 가지를 형성한다.
step3
prune data 로 가지치기를 수행한다.
상위 노드부터 차례대로 e 값을 측정한다.
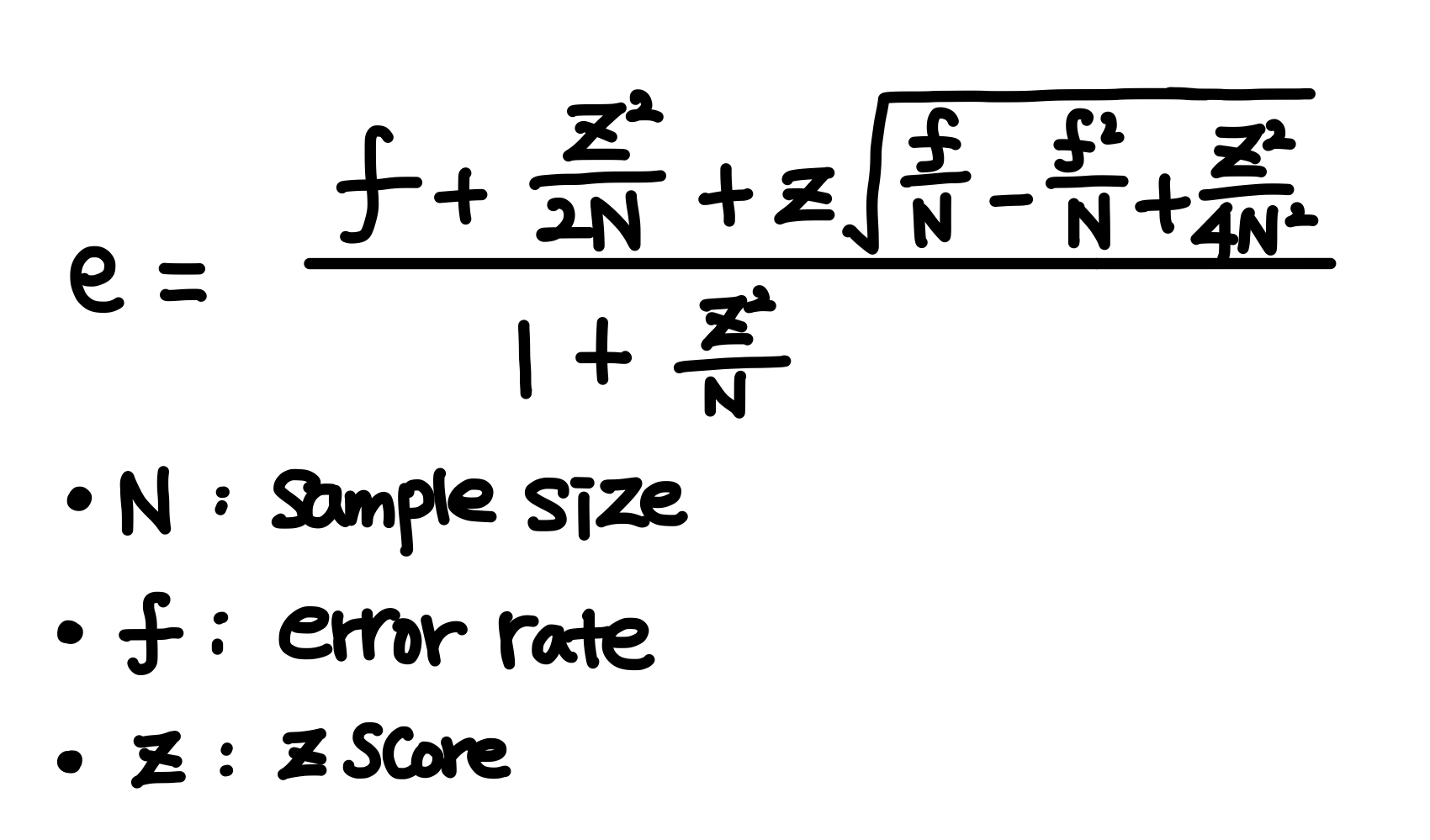
자식 노드들의 e 값의 가중치 합 > 부모 노드 e 이면, 해당 분기 진행하지 않고 가지치기 수행한다.
2. DecisionTreeClassifier 클래스
2.1 모델 훈련
트리 모델은 불순도가 낮아지는 방향으로 트리를 생성해간다.
DecisionTreeClassifier 생성 시 매개 변수 max_depth 설정 안 할 경우, 모든 클래스가 순수할 때까지 트리 생성한다.
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
X = iris.data[:, 2:]
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2)
tree_clf.fit(X, y)
2.2 클래스 확률 추정
결정 트리는 한 샘플이 특정 클래스 k 에 속할 확률을 추정할 수 있다.
predict_prob() 를 통해 클래스 확률 추정한다.
predict() 를 통해 클래스를 추정한다.
이때 predict_prob() 가 가장 높은 클래스로 할당한다.
#새로운 샘플의 클래스 확률 추정
print(tree_clf.predict_prob([5, 1.5]))
#새로운 샘플의 클래스 추정
print(tree_clf.predict([5, 1.5]))
2.3 결정 트리 시각화
from sklearn.tree import export_graphviz
export_graphviz(
tree_clf,
out_file = image_path('iris_tree.dot')
feature_names = iris.feature_names[2,:],
class_names = iris.target_names,
rounded = True,
filled = True
)
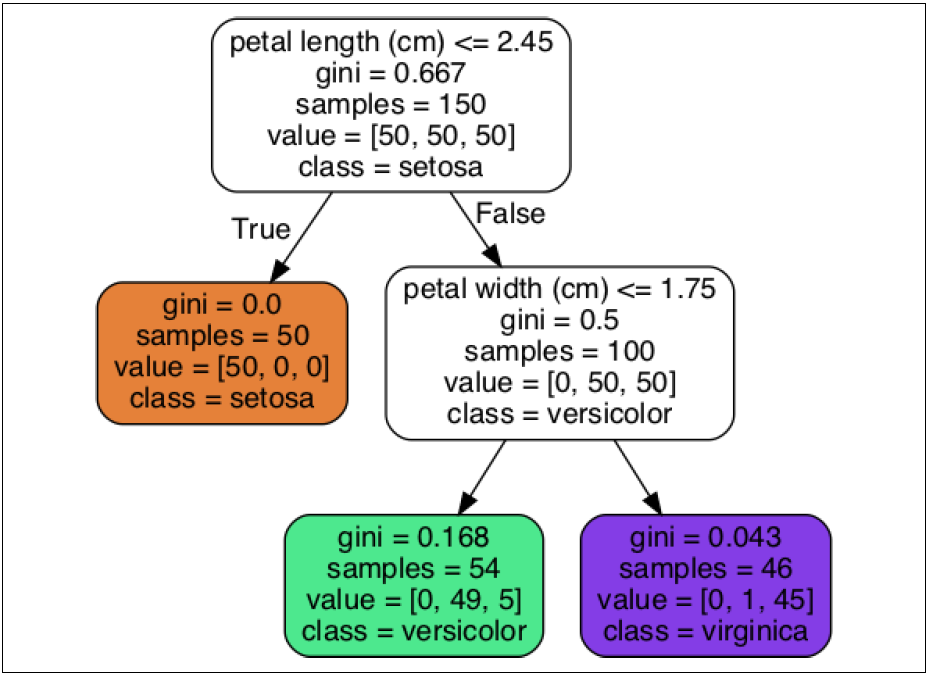
결정 트리 내 속성 의미
- samples : 해당 노드에 속하는 훈련 샘플 수
- value : 각 클래스 별 나뉠 훈련 샘플 수
- gini : 불순도 측정 값
cf. 모델 해석 : 화이트 박스와 블랙 박스
결정 트리는 직관적이고 결정 방식을 이해하기 쉽다.
이런 모델을 화이트 박스 모델이라고 한다.
반대로 랜덤포레스트나 신경망은 블랙박스 모델이다.
이 알고리즘들은 성능이 뛰어나고 예측을 만드는 연산 과정을 쉽게 확인할 수 있지만
왜 그런 예측을 만드는 지 쉽게 설명하기 어렵다.
3. 결정 트리 규제
트리 모델 생성은 Recursive Partition 을 통해 이뤄진다.
Recursive Partition은 leaf node 가 100% Purity 갖을 때까지 Full Tree를 생성한다.
하지만 Full Tree 즉 학습 데이터를 완벽하게 분리한다는 것은 y = f(x) + e 일때 e (noise) 까지 모두 학습했다는 의미이다.
e ( noise)는 데이터마다 random하게 다르기에 e 까지 학습하면 새로운 데이터에 대한 예측 성능이 떨어진다.
다시 말해 Full Tree는 Overfitting 되는 경향을 가져 Poor Generalization ability 를 갖는다.
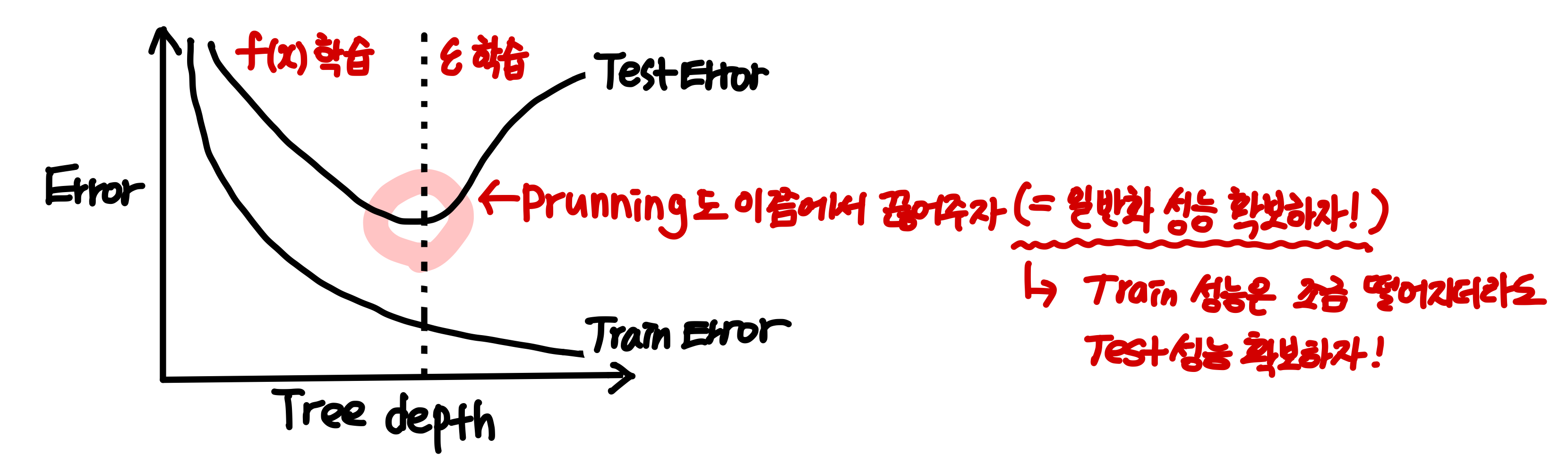
이에 Tree 모델의 일반화 성능 확보를 위한 다양한 규제 방법에 대해 살펴보자.
3.1 매개 변수
결정 트리는 훈련 데이터에 대한 제약 사항이 거의 없다.
(예를 들어, 선형 모형은 데이터가 선형일 거라는 제약 사항 등)
다만, 트리 모델은 훈련 데이터에 민감하다.
트리 모델 생성 시 별 다른 규제 설정 안 할 경우, 트리 모델은 마지막 leaf 노드가 순수해질 때까지 트리 모델을 생성한다.
이렇게 훈련 데이터에 너무 과하게 훈련된 과대 적합 모델을 생성하게 된다.
따라서 트리 모델은 적절하게 규제해야 한다.
DecisionTreeClassifier 에는 결정 트리의 형태를 제한하는 매개 변수가 몇 개 있다.
˙ max_depth : 결정 트리의 최대 깊이
˙ min_samples_split : 분할되기 위해 노드가 갖고 있어야 하는 최소 샘플 수
˙ min_samples_leaf : 리프 노드가 가지고 있어야 하는 최소 샘플 수
˙ max_leaf_nodes : 리프 노드의 최대 수
대체적으로 min_ 매개 변수를 추가하거나 max_ 매개 변수를 제한하면 모델에 규제가 커진다.
그렇다면 어떤 매개 변수를 어느 정도 설정해야 할까?
가장 일반적인 방법은 다양한 파라미터의 조합에 대한 그리드 탐색을 통해 모델 훈련시킨 후, 교차 타당성 검사를 통해 홀드 아웃 데이터에서의 에러가 최소가 되는 조합을 선정한다.
3.2 가지치기 알고리즘
(1) 사전 가지치기
트리 생성을 미리 제한한다.
사이킷런의 DecisionTreeClassifier 는 early_stopping 으로 모델의 깊이, 가지 갯수 등의 하이퍼파라미터를 GridSearch를 통해 튜닝하는 방식으로 사전 가지치기를 진행할 수 있다.
(2) 사후 가지치기
제한 없이 결정 트리를 훈련 시키고 불필요한 노드를 제거하는 방식이다.
순도를 높이는 것이 통계적으로 효과가 없다면 리프 노드 바로 위의 노드는 불필요할 수 있다.
대표적으로 chi-squared test 와 같은 통계적 검정을 사용하여 우연히 향상된 것인지 추정할 수 있다.
p-value 값이 어떤 임계값 (통상적으로 5%) 보다 높으면 그 노드는 불필요한 것으로 간주되고 그 자식 노드는 삭제된다.
사후 가지치기는 불필요한 노드가 없어질 때까지 계속된다.
사이킷런의 DecisionTreeClassifier 는 cost_complexity_prunning_path 를 활용하여 사후 가지치기를 진행할 수 있다.

clf = DecisionTreeClassifier()
path = clf.cost_complexity_prunning_path(X_train, y_train)
# ccp_alpha 가 증가할수록 impurities 증가하고 leaf_node 수 감소하고 depth 얕아진다.
ccp_alphas = path.ccp_alphas
impurities = path.impurities
'Machine Learning > 2. 지도 학습 알고리즘' 카테고리의 다른 글
| [모델 알고리즘][앙상블 학습] 배깅, 페이스팅 (0) | 2021.08.13 |
|---|---|
| [회귀] 결정 트리 회귀 모델 (0) | 2021.08.13 |
| [모델 알고리즘] 서포트 벡터 머신 - SVM 이론 (0) | 2021.08.09 |
| [모델 알고리즘] 서포트 벡터 머신 - SVM 회귀 (0) | 2021.08.09 |
| [모델 알고리즘] 서포트 벡터 머신 - 비선형 SVM 분류 (0) | 2021.08.09 |



