My Data Story
[군집] K-평균 본문
◈ '군집' 목차 ◈
1. K-평균
K-평균 알고리즘에 대해 이해하고, 센트로이드 초기화, 최적의 클러스터 개수 선정하는 방법 등에 대해 알아보자.
1. K-평균
K-평균은 데이터를 K개의 클러스터로 나눈다.
이때 할당된 클러스터의 평균과 포함된 데이터들의 거리 제곱합이 최소가 되도록 한다.
K평균은 각 클러스터의 크기가 동일하다는 보장은 없지만 클러스터끼리 최대한 멀리 떨어지도록 한다.
사이킷런에서 KMeans 을 통해 K-평균 모델을 구현할 수 있다.
알고리즘이 찾을 클러스터 개수 K를 지정하면, 각 클러스터의 중심을 찾고 가장 가까운 클러스터에 샘플을 할당한다.
KMeans 가 갖는 몇 가지 속성에 대해 살펴보면 ...
- labels_ : 군집에서 각 샘플이 속하는 클러스터 인덱스를 리턴한다.
- cluster_centers_ : 알고리즘이 찾은 각 클러스터의 센트로이드를 리턴한다.
Kmeans 는 predict() 호출 시 새로운 샘플에 가장 가까운 센트로이드의 클러스터에 할당하고
transform() 호출 시 샘플과 각 센트로이드 사이 거리를 반환한다.
from sklearn.cluster import KMeans
k = 5
kmeans = KMeans(n_clusters=k)
y_pred = kmeans.fit_predict(X)
print(kmeans.labels_)
print(kmeans.cluster_centers_)
print(kmeans.predict(X_new))
print(kmeans.transform(X_new))
K-평균 알고리즘은 클러스터의 크기가 많이 다르면 잘 작동하지 않는다.
샘플을 클러스터에 할당할 때 센트로이드까지 거리를 고려하는 것이 전부이기 때문이다.
2. K-평균 알고리즘
K-평균 알고리즘은 할당된 클러스터의 센트로이드와 포함된 데이터들 간의 거리 제곱합이 최소가 되도록 한다.
step1
센트로이드를 랜덤하게 선정한다.
step2
각 샘플을 가장 가까운 센트로이드의 클러스터로 할당한다.
step3
각 클러스터에 할당된 샘플들의 평균을 구해 센트로이드를 업데이트 한다.
step4
step2 ~ step3 과정을 반복하다, 더 이상 센트로이드 변화가 없을 때까지 위 과정을 반복한다.

데이터가 군집할 수 있는 구조를 가진다면, 알고리즘의 계산 복잡도는 샘플 개수, 클러스터 개수, 차원 개수에 선형적이다.
그렇지 않다면 최악의 경우 계산 복잡도는 지수적으로 증가할 수도 있다.
실전에서 이런 상황은 드물다. 일반적으로 k-평균은 가장 빠른 군집 알고리즘 중 하나이다.
k-평균 알고리즘은 수렴하는 것은 보장되지만, 최적의 솔루션이라는 보장은 못 한다. 즉 지역 최적점으로 수렴할 수 도 있다.
이 여부는 센트로이드 초기화에 달려 있다.
3. 센트로이드 초기화 방법
■ 방법1
센트로이드 위치를 근사하게 알 수 있다면, init 매개 변수에 센트로이드 리스트를 담은 넘파이 배열을 지정하고 n_init를 1로 설정할 수 있다. (init 은 초기 센트로이드 포인트이고, n_init은 센트로이드 초기화 횟수)
good_init = np.array([[-3,3], [-3,2], [-3,1], [-1,2], [0,2]])
kmeans = KMeans(n_clusters=5, init=good_init, n_init=1)
■ 방법2
랜덤 초기화를 다르게 하여 여러 번 알고리즘을 실행하고 가장 좋은 솔루션을 선택한다.
그렇다면, 가장 좋은 솔루션임을 어떻게 알 수 있을까?
각 샘플과 가장 가까운 센트로이드 사이의 평균 제곱 거리 합인 이너셔 intertia 값을 성능지표로 사용한다.
모델 이너셔가 가장 작은 모델을 선택한다.
이너셔가 작을 수록 해당 클러스터 내부 샘플들이 모여 있다는 의미이기 때문이다.
위 과정을 사이킷런 KMeans 에서 작동하는 관점에서 설명하면 다음과 같다.
step1
KMeans 생성 시 매개 변수 n_init 을 통해 랜덤 초기화 횟수를 설정한다.
step2
fit() 호출하기 전에 n_init 만큼 K-means 알고리즘을 실행한 후 inertia 값이 가장 적은 모델을 선택한다.
step3
fit() 호출한 후 KMeans 의 속성 inertia_ 에 모델의 이너셔가 저장된다. score() 함수는 inertia_ 값에 (-) 부호가 붙은 값을 리턴한다. 모델이 좋을 수록 score 값이 높도록 설정되어 있는 사이킷런 특성 때문이다.
kmeans = KMeans(n_clusters=5, n_init=50)
print(kmeans.initia_)
print(kmeans.score())
■ 방법3
데이비드 아서와 세르게이 바실비츠키가 2006년 k-평균 알고리즘을 향상시킨 k-평균++ 알고리즘을 제안했다. 이 알고리즘은 다른 센트로이드와 거리가 먼 센트로이드를 선택하는 똑똑한 초기화 단계를 거친다. 이 방법으로 k-평균 알고리즘이 최적이 아닌 솔루션으로 수렴할 가능성을 크게 낮추게 되었다.
K-평균 ++ 알고리즘 센트로이드 초기화 과정은 다음과 같다.
step1
데이터 셋에서 무작위로 균등하게 하나의 센트로이드 c(1) 을 선택한다.
step2
P(x(i)) 확률로 샘플 x(i)를 새로운 센트로이드 c(i)로 선택한다. 이 확률 분포는 이미 선택한 센트로이드에서 멀리 떨어진 샘플을 다음 센트로이드로 선택할 가능성을 높인다. P(x(i)) 에 대한 수식은 다음과 같다.

step3
k개의 센트로이드가 선택될 때까지 이전 단계를 반복한다.
K-평균 ++ 알고리즘은 P(x(i)) 등 추가 계산이 들지만, 최적 솔루션을 찾기 위해 알고리즘을 실행하는 반복 횟수를 줄일 수 있기 때문에 충분히 가치가 있다. 사이킷런에서 KMeans의 매개 변수 init = 'k-means++' 가 기본값이다.
4. k-평균 속도 개선과 미니배치 k-평균
2013년 찰스 엘칸의 논문에서 k-평균 알고리즘에 대해 또 다른 중요한 개선을 제안했다.
불필요한 거리 계산을 줄임으로서 알고리즘의 속도를 상당히 높였다.
삼각 부등식(AC <= AB + BC) 을 사용하고 샘플과 센트로이드 사이의 거리를 위한 하한선과 상한 선을 유지한다.
사이킷런에서 KMeans 클래스는 이 방식을 기본으로 설정한다.
이는 Kmeans의 매개 변수 algorithm = 'elkan' 에 해당한다.
2010년 데이비드 스컬리의 논문에서 k-평균 알고리즘의 또 다른 중요한 변종이 제시되었다.
전체 데이터 셋을 사용해 반복하지 않고 각 반복마다 미니 배치를 사용해 센트로이드를 조금씩 이동시킨다.
이는 일반적으로 알고리즘의 성능을 3~4배 정도 향상시킨다.
메모리에 들어가지 않는 대량의 데이터 셋에 군집 알고리즘 적용할 수 있다.
사이킷런에서 MiniBatchKMeans 클래스에 이 알고리즘이 구현되어 있다.
from sklearn.cluster import MiniBatchKMeans
minibatch_kmeans = MiniBatchKMeans(n_clusters=5)
minibatch_kmeans.fit(X)
이때 MiniBatchKMeans 를 사용하기 위해서는 X 데이터 셋이 주피터 노트북 메모리 상에 올릴 수 있어야 한다.
주피터 메모리에 올리는 것이 불가하다면, memmap을 활용할 수 있다.
filename = "cluster.data"
X_mm = np.memmap(filename, dtype='float32', mode='write', shape=X.shape)
X_mm[:] = X
minibatch_kmeans = MiniBatchKMeans(n_clusters=10, batch_size=10, random_state=42)
minibatch_kmeans.fit(X_mm)
또는 MiniBatchKMeans 클래스의 partial_fit() 을 통해 한 번에 하나의 미니 배치를 전달할 수 있다.
하지만 초기화도 여러 번 수행해야 하고 만들어진 결과에서 가장 좋은 것을 직접 골라야 해서 구현할 부분이 많다...
미니 배치 k-평균 알고리즘이 일반 k-평균 알고리즘보다 훨씬 빠르지만 이너셔는 일반적으로 조금 더 나쁘다.
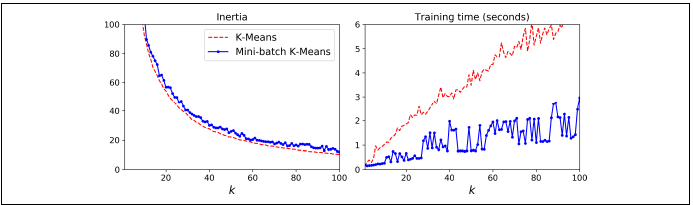
왼쪽 그래프를 보면, 두 곡선의 차이는 상당히 일정하게 유지되지만 k가 증가함에 따라 이너셔가 줄어들기 때문에 두 곡선의 차이가 차지하는 비율은 점점 커진다. 오른쪽 그래프를 보면, 미니 배치 k-평균이 일반 k-평균보다 훨씬 빠르고 k가 증가함에 따라 더 커지는 것을 볼 수 있다.
5. 최적의 클러스터 개수 찾기
일반적으로 클러스터 개수 k 를 어떻게 설정할 지 알 수 없다. 만약 올바르게 지정하지 않으면 결과는 매우 나쁘다.
쉽게 생각해서, 가장 작은 이너셔를 갖는 모델을 선택하면 되지 않을까? 싶지만...
이너셔는 k가 증가할 수록 무조건 감소하기 때문에 이너셔를 지표로 삼을 수 없다.
클러스터가 늘어날 수록 각 샘플은 센트로이드에 더 가까워지기 때문이다.
■ 방법1. 엘보 찾기
이너셔가 빠르게 감소하다 느려지는 변곡점을 선택한다. 하지만 이 방법은 조금 엉성하다.

■ 방법2. 실루엣 점수
실루엣 점수는 엘보 찾는 방법보다 정확하지만 계신 비용이 많이 든다.
실루엣 점수는 모든 샘플의 실루엣 계수의 평균이다.
샘플의 실루엣 계수는 (b-a)/max(a,b) 로 계산한다.
'a'는 동일한 클러스터에 있는 다른 샘플까지 평균 거리 (클러스터 내부 거리) 이고,
'b'는 자신이 속한 클러스터를 제외한 나머지 중 가장 가까운 클러스터의 샘플까지 평균 거리이다.
실루엣 계수는 -1 에서 +1 까지 바뀔 수 있다.
+1에 가까우면 자신의 클러스터 안에 잘 속해 있고 다른 클러스터와는 멀리 떨어져 있다는 의미이고,
0에 가까우면 클러스터의 경계에 있다는 의미이고,
-1에 가까우면 이 샘플이 잘못된 클러스터에 할당되었다는 의미이다.

from sklearn.metrics import silhouette_score
silhouette_score(X, kmeans.labels_)
실루엣 다이어그램은 모든 샘플의 실루엣 계수를 할당된 클러스터와 계숫값으로 정렬한 그래프이다.
˙ '그래프의 높이' : 클러스터가 포함하고 있는 샘플의 갯수
˙ '그래프 너비' : 클러스터에 포함된 샘플의 정렬된 실루엣 계수
˙ '그래프 수직 파선' : 실루엣 점수

클러스터의 샘플 대부분이 '수직 파선'보다 큰 것이 좋다.
클러스터의 샘플 대부분이 수직 파선보다 낮은 계수를 가지면 다른 클러스터랑 너무 가깝다는 의미이기 때문이다.
'그래프 너비'가 넓을 수록 좋기는 하지만, 더 중요한 것은 각 클러스터 별 그래프 높이가 균등한 것, 즉 비슷한 크기의 클러스터를 얻는 것이 좋다.
위 그래프로 비교했을 때, k=4일 때 전반적인 실루엣 계수가 높지만, 비교적 실루엣 계수도 높고 비슷한 크기의 클러스터가 존재하는 k=5 를 선택하는 것이 더 낫다.
6. k-평균 한계
k-평균은 속도도 빠르고 확장이 용이하나, k-평균이 완벽한 것은 아니다.
최적이 아닌 솔루션을 피하기 위해서는 알고리즘을 여러 번 실행해야 한다.
또한 클러스터 개수를 지정해줘야 한다. 꽤 번거로운 작업일 수 있다.
k-평균은 클러스터의 크기나 밀집도가 서로 다르거나 원형이 아닌 경우 잘 동작하지 않는다.
Tip!
k-평균을 실행하기 전에 입력 특성의 스케일 맞추는 것이 중요하다.
그렇지 않으면 클러스터가 길쭉해지고 k-평균 결과가 좋지 않다.
물론 특성 스케일을 맞추어도 모든 클러스터가 잘 구분되고 원형의 형태를 갖는다고 보자할 수는 없지만 일반적으로 더 좋아진다.
※ 데이터에 따라 잘 수행할 수 있는 군집 알고리즘이 다르다. ex. 타원형 클러스터에는 가우시안 혼합 모델이 잘 작동하는 등
'Machine Learning > 3. 비지도 학습 알고리즘' 카테고리의 다른 글
| [군집] HDBSCAN (0) | 2023.08.19 |
|---|---|
| [군집] DBSCAN (0) | 2023.08.19 |
| [차원 축소] t-SNE (0) | 2023.08.19 |
| [차원 축소] 지역 선형 임베딩 LLE (0) | 2023.08.19 |
| [차원 축소] 커널PCA (0) | 2021.08.13 |




