My Data Story
[차원 축소] PCA, 랜덤 PCA, 점진적 PCA 본문
◈ '차원 축소' 목차 ◈
2. PCA, 랜덤 PCA, 점진적 PCA
PCA, 랜덤 PCA, 점진적 PCA 에 대해 살펴보고, 적절한 축소 차원의 수를 결정하는 방법과 PCA 활용에 대해 알아보자.
PCA 주성분 분석은 가장 인기 있는 차원 축소 알고리즘이다.
데이터에 가장 가까운 초평면을 정의한 다음, 데이터를 이 평면에 '투영' 시킨다.
1. PCA 알고리즘
step1. 주성분 찾기
투영하기 전에 올바른 초평면을 선택해야 한다. 올바른 초평면은 분산이 최대로 보존되는 축에 투영한 것이다.
이는 분산이 최대로 보존되는 축을 선택하는 것이 정보가 적게 손실되기 때문이다.
다시 말해, 원본 데이터셋과 투영된 것 사이의 평균 제곱 거리를 최소화하는 축을 선택하는 것이 분산이 최대로 보존되는 축이다.
첫 번째 축 : PCA는 훈련 세트에서 분산이 최대인 축을 찾는다.
두 번째 출 : 첫 번째 축에 직교하고 남은 분산을 최대한 보존하는 축을 찾는다.
PCA는 주성분 방향을 가리키고 원점에 중앙이 맞춰진 단위 벡터이다.
하나의 축에 단위 벡터가 양 방향으로 2개라, PCA가 반환하는 단위 벡터의 방향이 일정하지는 않다.
대부분 같은 축에 놓여 있다.
※ 그렇다면, 훈련 세트의 주성분을 어떻게 찾을 수 있을까?
훈련 세트에 대한 공분산 행렬(Cov) 을 구한 후, 공분산 행렬에 대한 특잇값 분해(SVD)를 통해 구할 수 있다.
특잇값 분해(SVD) 를 통해 주성분 벡터를 유도하는 과정이 궁금하다면 아래 접힌 글을 참고하자.
(참조) 특잇값 분해를 통한 주성분 벡터 유도
공분산은 특성 간의 선형 관계를 측정한 지표로, 모든 특성에 대해 공분산을 모아 행렬로 표현한 것이 공분산 행렬이다.
공분산 행렬(Cov)을 표준 행렬 분해 기술인 특잇값 분해(SVD) 를 통해 훈련 세트 행렬 X를 3개의 행렬간의 행렬 곱셈 (U)(∑)(V^T) 로 분해할 수 있다.
공분산 행렬의 고유 벡터는 분산이 어느 방향으로 가장 큰 지 나타나 있다.
여기서 찾고자 하는 모든 주성분의 단위 벡터가 V에 담겨 있다.
이때 ∑ 는 대각선 성분을 제외한 나머지 값은 모두 0 으로, 분해한 각 특성의 값 크기는 대각행렬시그마 ∑ 에 의해 결정된다.
이렇게 주성분을 찾으면, 주성분으로 정의한 초평면이 선정된다.
공분산은 특성 간의 선형 관계를 측정한 지표로, 모든 특성에 대해 공분산을 모아 행렬로 표현한 것이 공분산 행렬이다.

공분산 행렬(Cov)을 표준 행렬 분해 기술인 특잇값 분해(SVD) 를 통해 훈련 세트 행렬 X를 3개의 행렬간의 행렬 곱셈 (U)(∑)(V^T) 로 분해할 수 있다.


공분산 행렬의 고유 벡터는 분산이 어느 방향으로 가장 큰 지 나타나 있다.
여기서 찾고자 하는 모든 주성분의 단위 벡터가 V에 담겨 있다.
이때 ∑ 는 대각선 성분을 제외한 나머지 값은 모두 0 으로, 분해한 각 특성의 값 크기는 대각행렬시그마 ∑ 에 의해 결정된다.

이렇게 주성분을 찾으면, 주성분으로 정의한 초평면이 선정된다.
Numpy 패키지에는 이미 특잇값 분해(SVD) 계산을 할 수 있는 함수가 구현되어있다.
np.linalg.svd() 을 통해 훈련 세트 X에 대한 특잇값 분해(SVD)를 적용하면 주성분이 구해진다.
PCA 는 데이터 셋의 평균이 0 이라고 가정한다. (원점에 맞춘다)
따라서 먼저 훈련 데이터를 원점에 맞춘 후 특잇값 분해 계산을 통해 주성분을 구하면 된다.
cf. 사이킷런의 PCA 파이썬 클래스는 데이터를 자동으로 원점으로 맞춰주어 신경쓰지 않아도 된다.
훈련 데이터에 대해 특잇값 분해 함수를 활용해 주성분을 구하는 코드는 다음과 같다.
X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centerd)
c1 = Vt.T[:, 0]
c2 = Vt.T[:, 1]
step2. d 차원으로 투영하기
d개의 주성분으로 정의한 초평면에 투영하여 데이터 셋의 차원을 d차원으로 축소시킨다.
이 초평면은 분산을 가능한 한 최대로 보존하는 투영임을 보장한다.

#SVD통해 구해진 주성분 중 첫번째, 두번째 성분을 주성분으로 정의
W2 = Vt.T[:,:2]
#W2로 정의한 초평면에 투영
X_d_proj = X_centerd.dot(W2)
※ PCA 역변환
PCA 역변환은 축소된 데이터를 원본의 차원 수로 되돌리는 과정이다.
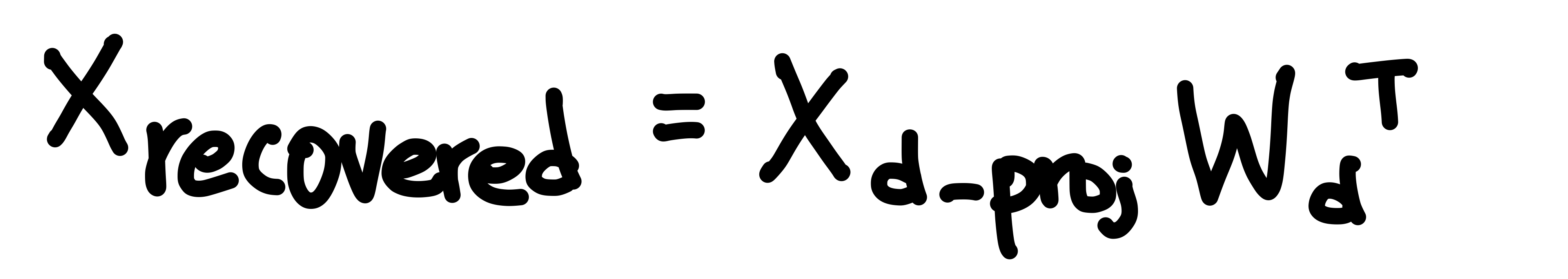
#SVD통한 역변환 구현
X_recover = X_d_proj.dot(Vt[:2, :])
2. PCA 모델 구현
2.1 PCA
사이킷런에서 PCA 클래스를 활용해 PCA 모델을 구현할 수 있다.
PCA 생성 시 축소하고자 하는 주성분 갯수는 매개 변수 n_components 로 설정한다.
이때, PCA 는 내부적으로 자동으로 데이터를 원점으로 맞춰주기 때문에 바로 X 넣어도 된다.
from sklearn.decomposition import PCA
#n_components : 축소하고자 하는 주성분 갯수
pca = PCA(n_components = 2)
#PCA 내부에서 데이터 원점 맞추는 과정 자동으로 수행해서 그냥 X 넣어도 됨
X_d_proj = pca.fit_transform(X)
#components_ 속성에 Wd의 전치가 담겨 있다.
print(pca.components_)
원래 데이터를 X, d 차원의 평면으로 투영된 데이터를 X_d_project 라 할 때, PCA 의 inverse_transform(X_d_project) 를 통해 X에 대한 재구성 데이터 X_recoverd 를 구할 수 있다. 이때 재구성 데이터(압축 후 원복한 것) 과 원래 데이터 사이의 평균 제곱 거리를 재구성 오차라 한다.
재구성 오차가 존재한다는 것은 재구성된 데이터가 원본 데이터와 완전히 똑같지 않음을 의미한다. 그 이유는 투영하는 과정에서 일부 정보가 소실되었기 때문이다. 이는 PCA 가 투영 시 자동으로 데이터를 원점으로 맞추는 과정에서 소실된다고 볼 수 있다.
X_recoverd = pca.inverse_transform(X_d_proj)
2.2 랜덤 PCA
사이킷런에서 PCA의 매개 변수 svd_solver 를 'randomized' 로 설정하면, 확률적 알고리즘을 사용해 처음 d개의 주성분에 대한 근삿값을 빠르게 찾아간다. 이 알고리즘의 계산 복잡도는 완전한 SVD 방식인 O(m x n^2) + O(m^3) 이 아니라, O(m X d^2) + O(d^3) 이다. 따라서 d가 n보다 많이 작을 수록 완전한 SVD 보다 훨씬 빨라지게 된다.
rnd_pca = PCA(n_components=154, svd_solver='randomized')
X_reduced = rnd_pca.fit_transform(X_train)
PCA의 svd_solver 기본값은 'auto' 인데, m이나 n이 500보다 크고 d가 m이나 n의 80% 보다 작으면 자동으로 랜덤 PCA 알고리즘을 사용한다.
2.3 점진적 PCA
PCA 구현의 문제는 SVD 알고리즘을 실행하기 위해 전체 훈련 세트를 메모리에 올려야 한다는 것이다.
다행히 점진적 PCA 알고리즘이 개발되었다.
훈련 세트를 미니 배치로 나눈 뒤 IPCA 알고리즘에 한 번에 하나씩 주입한다.
이런 방식은 훈련 세트의 클 때 유용하고 온라인(새로운 데이터가 준비되는 대로 실시간) PCA를 적용할 수도 있다.
직접 구현하는 방법 두 가지가 있다.
■ 방법1
직접 훈련 세트를 여러 배치로 나누고 사이킷런 IncremenalPCA 파이썬 클래스에 주입하여 partial_fit() 하는 방법이 있다.
from sklearn.decomposition import IncrementalPCA
n_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_train, n_batches) :
inc_pca.partial_fit(X_batch)
X_reduced = inc_pca.fit_transform(X_train)
■ 방법2
Numpy의 memmap 파이썬 클래스를 사용하면, 하드 디스크의 이진 파일에 저장된 매우 큰 배열을 메모리에 들어 있는 것처럼 다룰 수 있다. IncrementalPCA 모델에 memmap 에 담은 훈련 데이터를 넣어 fit() 호출 하면, 자동으로 전체 훈련 데이터를 batch_size 만큼씩 미니 배치로 나눠 partial_fit() 을 호출하여 진행된다.
from tempfile import mkdtemp
import os.path as path
#filename 정의
filename = path.join(mkdtemp(), 'newfile.dat')
m = sample size 로 정의
n = feature size 로 정의
n_batches = mini batch 갯수 로 정의
X_mm_w = np.memmep(filename, dtype='float32', mode='write', shape=(m,n))
X_mm_w = X_train
X_mm_r = np.memmap(filename, dtype='float32', mode='read_only', shape(m,n))
batch_size = m // n_batches
inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size)
inc_pca.fit(X_mm_r)
3. 설명된 분산의 비율
PCA 의 explained_variance_ratio_ 속성을 통해 각 주성분의 설명된 분산의 비율을 알 수 있다.
이 비율은 각 주성분의 축을 따라 있는 데이터셋의 분산 비율을 나타낸다.

이때 1 - sum(pca.explained_variance_ratio_) 값은 재구성 오차 비율과 같다.

설명된 분산의 비율을 바탕으로 각 주성분이 데이터에 대한 정보를 얼마나 포함하고 있는 지 확인할 수 있다.
4. 적절한 차원 수 선택하기
■ 방법1
축소할 차원의 수를 임의로 정하기 보다
충분한 분산 (보통 95%) 이 될 때까지 차원을 추가하는 것이 가장 간단하다.
(물론 데이터의 시각화를 위해 축소하는 경우, 2개나 3개로 줄이는 것이 일반적이다.)
step1
차원을 축소하지 않고 PCA를 계산한 뒤 (fit_transform() 이 아닌 fit() 실행)
훈련 세트의 분산을 95%로 유지하는 데 필요한 차원의 수를 계산한다.
PCA 생성 시 n_components 를 설정하지 않으면 샘플 수와 특성 수 중 작은 값으로 설정된다.
pca = PCA()
pca.fit(X_train)
cumsum = np.cunsum(pca.explained_variance_ratio_)
d = np.argmax(cumsum >= 0.95) + 1
step2
적절한 차원 수 d 가 도출되면, n_components=d로 설정하여 PCA 를 다시 실행한다.
하지만 유지하려는 주성분의 수를 지정하기 보다
보존하려는 분산의 비율을 n_components 에 0.0 ~ 1.0 사이로 설정하는 편이 낫다.
즉 사이킷런 PCA는 n_components 에 정수넣으면 축소할 차원 수, 비율 넣으면 분산의 설명력으로 인식한다.
pca = PCA(n_components = 0.95)
X_reduced = pca.fit_transform(X_train)
■ 방법2
설명된 분산을 차원 수에 대한 함수로 그리는 것이다. 설명된 분산의 cumsum 을 그래프로 그린다.
설명된 분산의 빠른 성장이 멈추는 변곡점이 있다면, 해당 지점에서 차원을 축소해도 설명된 분산을 크게 손해보지 않을 것이다.

5. PCA 활용
5.1 Composition
차원을 축소하게 되면 훈련 세트의 크기는 줄어든다.
이런 크기 축소는 SVM 같은 분류 알고리즘의 속도를 크게 높일 수 있다.
물론, 항상 PCA 적용하기 전에 raw data로 할 수 있는 대안 모든 것을 실행해봐야 한다.
실행 중 메모리 상의 문제 등 발생할 경우, PCA 추천한다.
5.2 Visualization
데이터 시각화하는데 활용되기도 한다.
5.3 PCA 잘못된 활용
과대 적합을 방지하기 위해서 PCA 활용하는 것은 아주 잘못된 접근이다.
과대 적합 방지를 위해서는 정규화 기법을 하는 것이 바람직하다.
그 이유는 PCA 는 label(Y)를 고려하지 않고 X 데이터만을 보고 분산을 최대한 유지하도록 축소하는 기법이기 때문이다.
반면, 정규화는 label(Y) 와의 적합을 고려하는 규제이다.
'Machine Learning > 3. 비지도 학습 알고리즘' 카테고리의 다른 글
| [군집] K-평균 (0) | 2023.08.19 |
|---|---|
| [차원 축소] t-SNE (0) | 2023.08.19 |
| [차원 축소] 지역 선형 임베딩 LLE (0) | 2023.08.19 |
| [차원 축소] 커널PCA (0) | 2021.08.13 |
| [차원 축소] 투영, 매니폴드 (0) | 2021.08.13 |




