[차원 축소] 투영, 매니폴드

◈  '차원 축소' 목차 ◈

1. 투영, 매니폴드

     차원의 저주를 살펴보고, 차원 축소하는 2가지 방법 투영, 매니폴드의 컨셉에 대해 알아보자.

2. PCA, 랜덤 PCA, 점진적 PCA

3. 커널 PCA

4. MDS, Isomap

5. 지역 선형 임베딩 LLE

6. t-SNE

 

---

1. 차원의 저주

많은 경우 머신러닝 문제는 훈련 샘플 각각이 수천 심지어 수백만 개의 특성을 가지고 있다.

이런 많은 특성은 훈련을 느리게 할 뿐만 아니라, 좋은 솔루션을 찾기 어렵게 만든다.

이런 문제를 종종 차원의 저주라고 한다. 

 

훈련 세트의 차원이 클수록 과대 적합 위험이 커진다.

이론적으로 차원의 저주를 해결하는 방법은 훈련 샘플의 밀도가 충분히 높아질 때까지 훈련 세트의 크기를 키우는 것이다.

하지만 불행히도 차원의 수가 커짐에 따라 필요한 샘플의 크기가 기하급수적으로 늘어난다. 

 

 

차원을 축소시키면 일부 정보가 유실된다. 그래서 훈련 속도는 빨라질 수 있지만 성능은 조금 나빠질 수 있다. 

그러므로 차원 축소를 고려하기 전에 훈련이 너무 훈련이 너무 느린지 원본 데이터로 훈련해봐야 한다.

어떤 경우에는 차원 축소시키면 잡음이나 불필요한 세부 사항을 걸러내지만 일반적으로 속도만 빨라지는 경우가 많다. 

 

 

2. 차원 축소를 위한 접근 방법

구체적인 차원 축소 알고리즘을 살펴보기 전에, 차원을 감소시키는 두 가지 주요한 접근법인 '투영' 과 '매니폴드' 학습을 살펴보자.

2.1 투영

실전 문제에서 대부분의 특성은 거의 변화가 없는 반면, 몇몇 특성은 강하게 연관되어 있다.

결과적으로 모든 훈련 샘플이 고차원 공간 안의 저차원 부분 공간에 놓여 있다. 

 

예를 들어, 원 모양을 띄는 3차원 데이터 셋이 있다고 하자.

이 데이터들은 고차원(3D) 공간에 있는 저차원(2D) 부분 공간에 놓여 있다.

 

<2차원에 가깝게 배치된 3차원 데이터 셋>

 

 

여기서 모든 훈련 샘플을 부분 공간에 수직으로 투영하면 2D 데이터 셋을 얻을 수 있다.

각 축은 새로운 Z1과 Z2에 대응하게 된다. 

 

<투영하여 만들어진 새로운 2D 데이터 셋>

 

 

그러나 차원 축소에 있어 투영이 언제나 최선의 방법은 아니다. 

 

<부분 공간이 휘어지고 뒤 틀린 데이터 셋 - 스위스 롤>

 

 

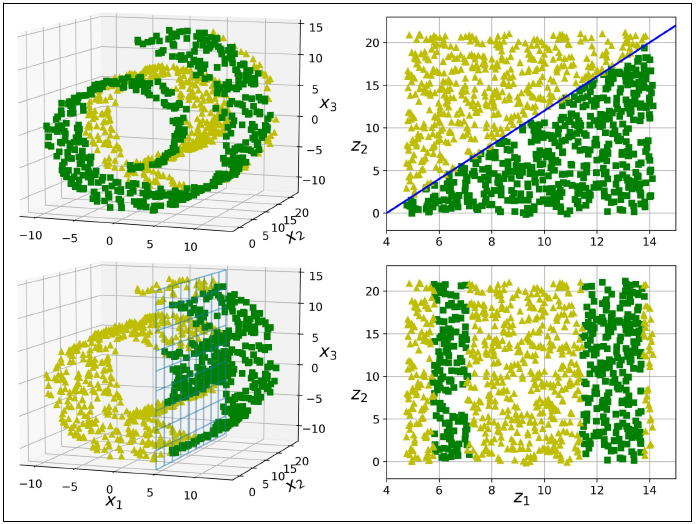
위 그림처럼 부분 공간이 뒤틀리거나 휘어 있는 경우, 투영하면 데이터들이 서로 뭉게진다( 아래 왼쪽 그래프).

이럴 경우, 데이터를 투영시키기 보다, 휘어 있는 부분 공간을 펼쳐서 2D 데이터 셋을 만드는 것이 좋다(아래 오른쪽 그래프).

이러한 접근 방식이 매니폴드 학습 이다.

 

<왼쪽 - 부분공가 투영 시 뭉개짐, 오른쪽 - 말린 부분공간 펼치기>

 

2.2 매니폴드 학습

위에서 살펴본 스위스 롤은 2D 매니폴드이다. 즉 2D 매니폴드는 고차원 공간에서 휘어지거나 뒤틀린 2D 모양이다. 

더 일반적으로 d차원 매니폴드는 국부적으로 d차원 초평면으로 보일 수 있는 n차원 공간의 일부이다.(d<n)

 

많은 차원 축소 알고리즘이 훈련 샘플이 놓여 있는 매니폴드를 모델링하는 식으로 작동한다. 이를 매니폴드 학습이라고 한다.

 

이는 대부분 실제 고차원 데이터셋이 더 낮은 저차원 매니폴드에 가깝게 놓여있다는 매니폴드 가정에 근거한다. 

매니폴드 가정은 종종 암묵적으로 다른 가정과 병행되곤 한다.

바로 '처리해야 할 작업(분류, 회귀)이 저차원의 매니폴드 공간에 표현되면 더 간단해질 것' 이란 가정이다.

 

하지만 이런 암묵적인 가정이 항상 유효한 것은 아니다. 오히려 더 복잡할 수도 있다. 

 

<저차원에서 항상 간단하지 않은 결정 경계>