My Data Story
[분류] 로지스틱 회귀 본문
◈ '분류' 목차 ◈
3. 로지스틱 회귀
로지스틱 회귀 모델을 통해 각 클래스에 속할 확률을 추정하는 과정에 대해 알아본다.
로지스틱 회귀 모델의 비용 함수에 대해 알아본다.
로지스틱 회귀 모델의 회귀 계수를 해석하는 방법에 대해 알아본다.
1. 클래스 추정 확률
로지스틱 회귀의 목표는 두 클래스를 잘 구분하는 결정 경계 Decisionboundary 를 구하는 것이다.
결정 경계는 입력 특성들의 선형 결합으로 표현되고
두 클래스는 결정 경계보다 위에 있는 클래스 (y=1) 와 결정 경계보다 아래에 있는 클래스 (y=0)로 구분된다.

결정 경계의 점수를 0~1 사이의 확률 형태로 만들기 위해 선형 결합값에 sigmoid 함수를 취한다.
이는 곧 y=1 인 클래스에 속할 확률이 된다.

각 샘플에 대해 클래스 추정 확률를 구한 후, 클래스를 구분하는 cut-off 확률과 비교한다.
클래스 추정 확률 h(x) >= 클래스 cut-off 확률이면, y=1 클래스에 할당하고
클래스 추정 확률 h(x) < 클래스 cut-off 확률이면, y=0 클래스에 할당한다.
기본적으로 클래스 cut-off 확률을 0.5로 설정한다.

클래스 cut-off 확률을 0.5로 설정한다는 것은 결정경계 점수 = 0 ( t = 0 ) 인 부분을 기준으로 클래스를 구분하겠다는 의미이다.

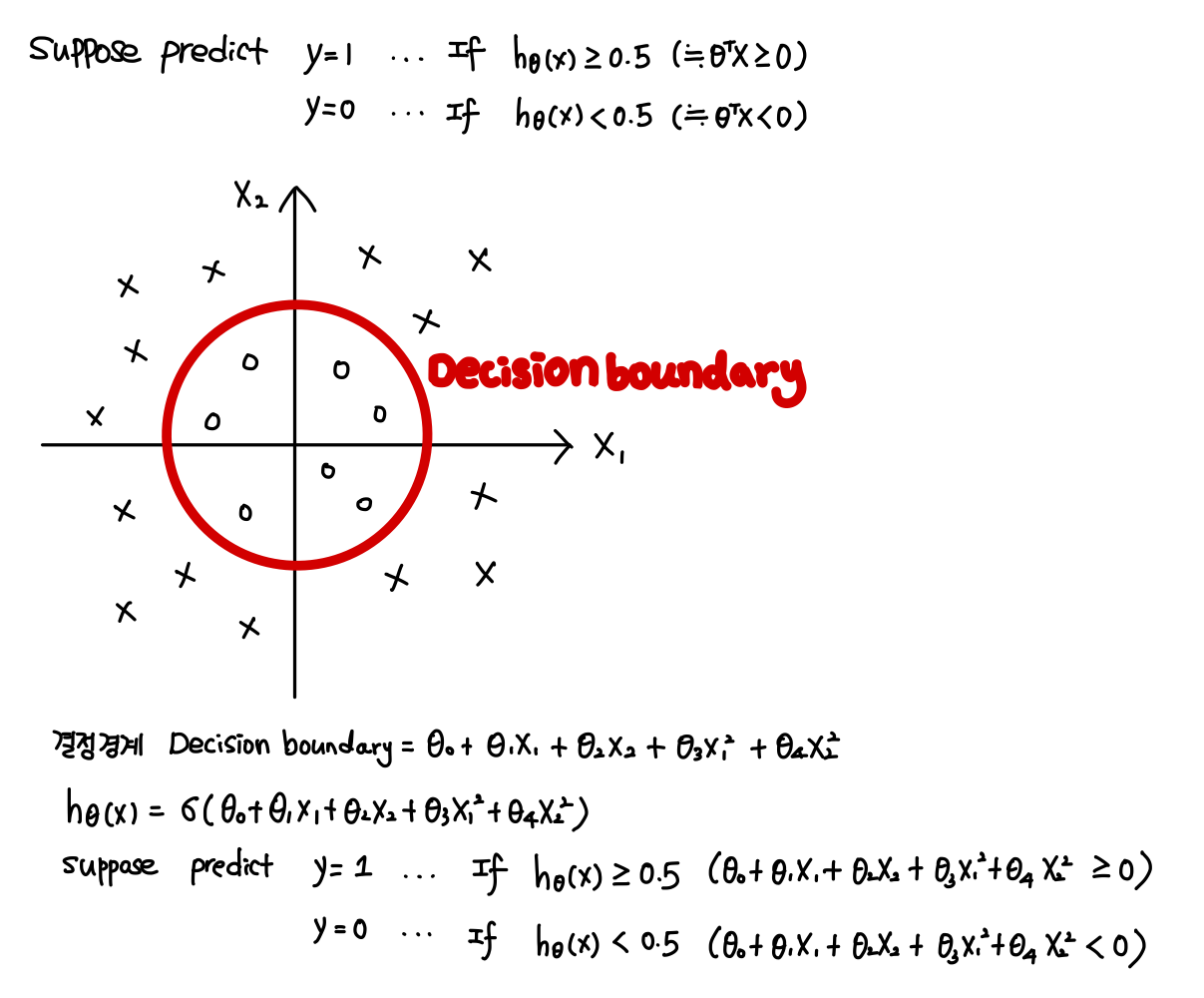
cf. 만약 클래스를 구분하는 결정 경계가 비선형 모양일 경우, 로지스틱 회귀 모델을 어떻게 될까?
˙결정 경계에 대한 다항 회귀식을 구현한 후, 시그모이드 함수를 취해 클래스 추정 확률을 계산하면 된다.
2. 훈련과 비용 함수
훈련의 목적은 양성 샘플 (y=1) 에 대해서 높은 확률로 추정하고, 음성 샘플 (y=0) 에 대해서 낮은 확률로 추정하는 모델의 파라미터 벡터를 찾는 것이다.
로지스틱 회귀 모델의 손실 함수(비용 함수) 은 선형 회귀 모델의 손실 함수와 밀접한 관련이 있다.
로지스틱 회귀 모델의 손실 함수를 선형 회귀 모델의 손실 함수로부터 유도해보면 다음과 같다.

그런데 sigmoid 함수는 Non-Convex 함수이다. 따라서 sigmoid 함수를 적용한 로지스틱 회귀 모델의 비용 함수 역시 Non-Convex 함수이다. Global 최저점을 찾기 위해서는 손실 함수는 Convex 함수여야 한다.
양성 샘플(y=1)에 대해 높은 확률로 추정하면 (1에 가깝게) 비용 함수가 낮도록
음성 샘플 (y=0)에 대해 낮은 확률로 추정하면 (0에 가깝게) 비용 함수가 낮도록
로지스틱 회귀 모델의 목표에 맞는 Convex 손실 함수를 생성하면 다음과 같다.

위 Convex한 비용 함수를 바탕으로 전체 훈련 샘플에 대한 비용 함수를 정리하면 다음과 같다.

이 비용 함수의 최솟값을 계산하는 정규 방정식 해는 없다.
경사 하강법을 통해 최적 파라미터를 찾아야 한다.
이 비용함수는 Convex 함수 (볼록 함수)라 경사 하강법이 전역 최솟값을 찾는 것을 보장한다.
(물론, 학습률이 너무 크지 않고 충분히 기다릴 시간 있다면...)
경사 하강법을 통해 전역 최솟값을 찾기 위해서 로지스틱 회귀 모델 비용 함수에 대해 편미분한 편도 함수는 다음과 같다.

경사 하강법을 통해 전역 최솟값을 찾기 위해 다음과 같이 가중치 업데이트를 진행한다.

위의 로지스틱 회귀 모델 비용 함수에 대한 편도 함수를 참조했을 때, 로지스틱 회귀 모델의 가중치는 예측값과 실제값이 많이 다르면 더 많이 업데이트하고 더불어 가중치와 연관 있는 설명 변수의 값만 영향을 받아 가중치 업데이트 시킨다.
3. 로지스틱 회귀 모델 규제
다른 선형 모델처럼 로지스틱 회귀 모델도 규제할 수 있다.
사이킷런에서 LogisticRegression 은 penalty 와 C 매개 변수 통해 규제할 수 있다.
penalty는 규제 방식에 대한 매개변수로 l1, l2 , elasticnet 등으로 설정할 수 있다.
LogisticRegression 은 l2 penalty 를 기본값으로 한다.
C는 규제 강도를 조절하는 매개변수로 alpha 값의 역수와 동일하다. C = 1/alpha
따라서 C가 높을 수록 규제가 줄어든다. (alpha 값은 높을 수록 규제가 커진다.)
로지스틱 회귀 모델에 규제를 가할 경우, 비용 함수는 다음과 같다.

4. 계수와 오즈비 해석
로지스틱 회귀 모델의 장점 중 하나는 재계산 없이 새 데이터에 대해 빨리 결과를 계산할 수 있다는 점과 모델을 해석하기가 다른 분류 방법들에 비해 상대적으로 쉽다는 점이 있다.
로지스틱 회귀 모델의 계수를 해석하기 위해서 오즈비를 이해하는 것이 중요하다.
오즈는 사건이 발생할 확률을 사건이 발생하지 않을 확률로 나눈 비율 p/(1-p)이다. 로지스틱 회귀 모델 관점에서 확률 p는 y=1인 클래스에 속할 확률로 이해할 수 있다. 확률 p에 대한 결정 경계(h(X)) 식을 오즈(y=1) 에 대해 정리하면 log(오즈(y=1)) 이 결정 경계 선형 결합식임을 알 수 있다.

이를 활용하여 나머지 예측 변수는 고정한 채, 하나의 변수만 1 만큼 증가시켰을 때 변하는 Odds Ratio를 구하면 다음과 같다.

위 식을 통해 X1의 계수 b1은 'X1에 대한 오즈비의 로그 값' 임을 알 수 있다.
위 식을 정리하면 다음과 같다.

이는 다시 말해 다음과 같다.

오즈비 관련하여 예를 들면 신용 카드 빚을 갚을 지를 예측하는 로지스틱 회귀 모델을 생각해보자.
º 응답 변수
연체 여/부 (y=1 이면 연체, y=0 이면 연체 아님)
º 예측 변수
X1 = 대출 목적에 대한 범주형 변수 (0 이면 신용 카드 빚 갚기 위해, 1 이면 소규모 사업)
X2 = 소득에 대한 상환 비율인 연속형 변수
º 결정 경계
1.21226 * X1 + 0.8244 * X2
X1 계수에 대해 해석하면, 소규모 사업 목적으로(X1=1) 대출한 경우가 신용 카드 빛 갚기 위해(X1=0) 대출한 경우보다 exp(1.21226)=3.4 배 만큼 연체할 오즈비가 증가진다.
X2 계수에 대해 해석하면, 소득에 대한 상환 비율이 1 증가할 때마다 exp(0.8244)=1.09배 만큼 연체할 오즈비가 증가한다.
5. 결정 경계
로지스틱 회귀 모델에서 어떤 결정 경계를 기준으로 클래스를 구분할 지 정하는 것이 중요하다.
적절한 결정 경계 (cut-off) 를 찾기 위해 입력 변수 값에 따라 각 클래스에 포함된 확률 값을 그려내보자.
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
iris = dataset.load_iris()
list(iris.keys())
X = iris['data'][:,3:]
y = (iris['target'] == 2) #이진분류기 생성을 위한 라벨 생성
log_reg = LogisticRegression()
log_reg.fit(X,y)
X_new = np.linspace(0, 3, 1000).reshape(-1,1)
#X_new에 대해 클래스 별 추정확률 도출
y_prob = log_reg.predict_proba(X_new)
plt.plot(X_new, y_prob[:,1], 'g--', label='Iris virginia')
plt.plot(X_new, y_prob[:,0], 'b--', label='Not Iris Virginia')

두 개의 특성을 바탕으로 결정 경계를 확인할 수도 있다.

검정 점선은 결정 경계를 나타낸 것이다.
결정 함수 = log_reg.coef[0][0] * 꽃잎 길이 + log_reg.coef[0][1] * 너비 + log_reg.intercept[0]
(cf. 만약, 다중 레이블 분류라면 log_reg.coef[1][0] 값도 존재할 수 있다.)
5. (별첨) 이진분류기 - SGDClassifier
사이킷런에서 SGDClassifier를 통해 이진 분류기를 생성할 수 있다.
SGDClassifier는 Stochastic Gradient Descent를 solver로 사용하는 일반화 된 선형 분류기이다.
SGDClassifier는 일반화된 선형 분류기이기에 다양한 손실 함수를 취할 수 있다.
(ex. loss = hinge / log / modified_huber / squared_hinge / perceptron)
데이터 구조 및 상태에 맞는 적절한 손실 함수를 설정하면 된다.
SGDClassifier는 확률적 경사 하강법 분류기이기 때문에 매우 큰 데이터 셋에 효율적이다.
SGDClassifier 가 손실 함수로 'log'를 취한다면, LogisiticRegression두 모델과 동일한 결과를 만들어 낼 것이다.
다만 SGDClassifier 와 LogisticRegression 의 solver 에 차이가 있어 SGDClassifier 가 더 빠르게 훈련될 것이다.
LogisticRegression 에는 solver로 sgd 알고리즘이 없기 때문이다.
from sklearn.linear_model import SGDClassifier
X, y = mnist['data'], mnist['target']
y = y.astype(np.unit8)
print(X.shape())
print(y.shape())
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
sgd_clf = SGDClassifier(random_state=42) #random_state는 재현을 위해 설정
#y값이 5이면 Treu, 아니면 False 되도록 레이블 구성
y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)'Machine Learning > 2. 지도 학습 알고리즘' 카테고리의 다른 글
| [분류] 다중 레이블 분류, 다중 출력 분류 (0) | 2021.08.06 |
|---|---|
| [분류] 소프트맥스 회귀 (0) | 2021.08.06 |
| [분류] 선형판별분석(LDA) (0) | 2021.08.06 |
| [분류] 나이브 베이즈 (0) | 2021.08.06 |
| [회귀] 규제가 있는 선형 회귀 (0) | 2021.08.06 |




