My Data Story
[회귀] 규제가 있는 선형 회귀 본문
◈ '회귀' 목차 ◈
8. 규제가 있는 선형 회귀
규제가 있는 선형 모델 릿지 회귀, 라쏘 회귀, 엘라스틱넷에 대해 살펴보자.
더불어 조기종료를 통해 모델을 규제하는 색다른 방법에 대해서도 살펴보자.
1. 규제가 있는 선형 모델
과대 적합을 감소시키는 좋은 방법은 모델을 규제하는 것이다.
다항 회귀 모델에 규제를 가하는 방법은 다항식의 차수를 감소시키는 것이고
선형 회귀 모델에 규제를 가하는 방법은 모델 파라미터(가중치)를 제한하는 것이다.
1.1 릿지 회귀

규제 항이 비용 함수에 추가되어 릿지 회귀의 비용함수는 다음과 같다.

이는 학습 알고리즘을 데이터에 맞추는 것 뿐만 아니라, 모델의 가중치가 가능한 작게 유지되도록 하는 것이다.
알파는 모델을 얼마나 규제할 지 조절한다.
알파= 0 이면, 선형 회귀와 같아진다.
알파가 커질 수록, 직선에 가까워진다. 즉 분산이 줄고 편향이 증가하게 된다.

편향은 규제되지 않는다. 그래서 릿지 회귀의 비용 함수의 합 기호가 i=0 이 아니라 i=1 에서 시작한다.
릿지 회귀의 비용함수에는 모델 파라미터들도 포함되어 있어,
데이터 스케일을 맞추지 않으면 모델 파라미터의 스케일도 다양해진다.
결국 모델 파라미터 크기에 따라 비용 함수에 미치는 영향도가 커져, 모델이 잘못 훈련될 수 있다.
따라서 릿지 회귀 뿐 아니라 규제가 있는 모델은 대부분 입력 특성의 스케일링을 진행하도록 한다.
Tip!
일반적으로 훈련하는 동안 사용하는 비용함수와 테스트에서 사용하는 성능 지표는 다르다.
훈련에 사용되는 비용 함수는 최적화를 위해 미분이 가능해야 한다.
테스트에 사용되는 성능 지표는 최종 목표에 가능한 가까워야 한다.
ex. 릿지 회귀 - 훈련시킬 때는 위 비용함수를 활용하고, 성능 측정할 때는 MSE만을 활용한다.
로지스틱 회귀 - 훈련시킬 때는 로그 손실 비용 함수 활용하고, 성능 측정할 때는 정밀도/재현율 활용한다.
이제 릿지 회귀 계산을 해보자.
릿지 회귀를 계산하기 위해 선형 회귀와 마찬가지로 정규 방정식을 사용할 수도 있고, 경사 하강법을 사용할 수 있다.
(1) 릿지 회귀 계수 추정 - 정규 방정식
릿지 회귀 모델의 파라미터 계산을 위해, 정규 방정식의 해를 직접 구할 수 있다.
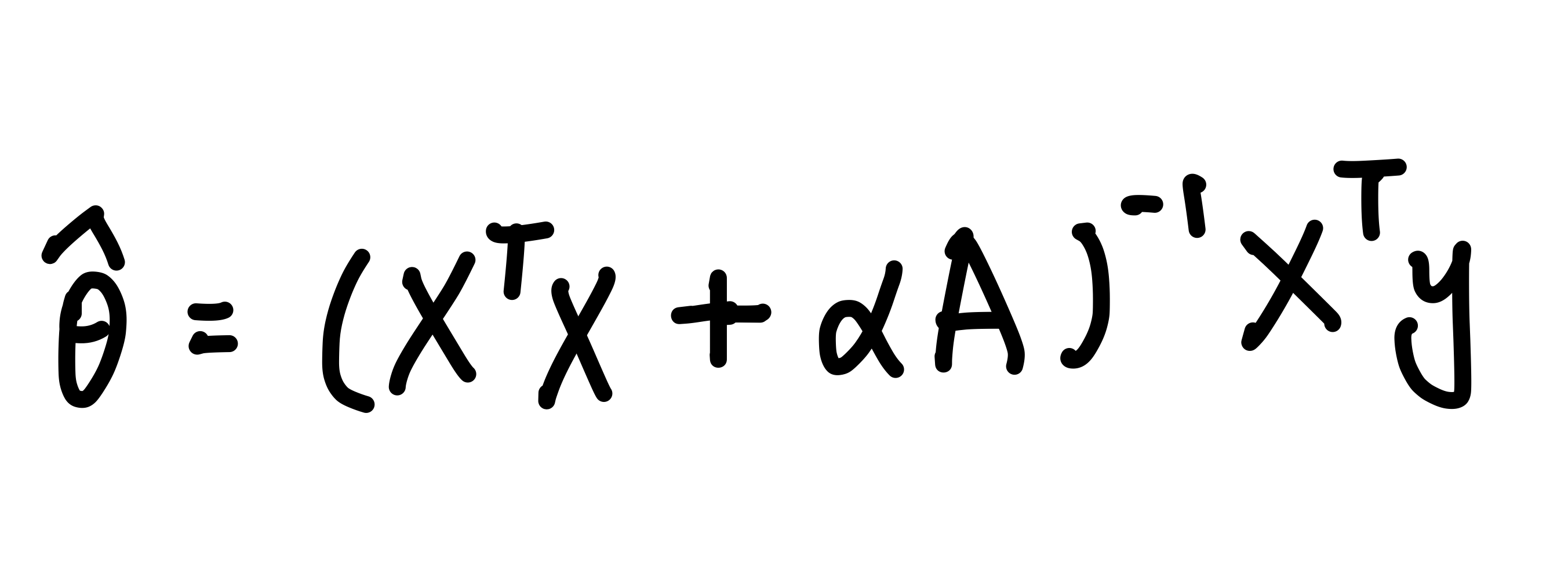
사이킷런에서 Ridge를 사용하면 정규 방정식 해를 구하는 식으로 작동한다.
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver='cholesky')
ridge_reg.fit(X,Y)
ridge_reg.predict([[1.5]])
(2) 릿지 회귀 계수 추정 - 경사 하강법
사이킷런에서 SGDRegressor 를 사용하면 확률적 경사 하강법을 활용한다.
이때 penalty 파라미터를 l2로 설정하면 라쏘 회귀를 구할 수 있다.
from sklearn.linear_model import SGDRegressor
#확률적 경사 하강법 활용 + 가중치 벡터에 대한 규제 적용
sgd_reg = SGDRegressor(penalty='l2')
sgd_reg.fit(X,Y.ravel())
sgd_reg.predict([[1.5]])
SGDRegressor 을 생성하고 fit() 시키면 확률적 경사 하강법을 활용하여 모델 파라미터를 계산한다.
이 계산 과정을 수식으로 표현하면 다음과 같다.
(아래 수식은 참고 사항이니, 이해가 안된다면 그냥 넘어가도록 하자. )

Tip!
일반적으로 훈련하는 동안 사용하는 비용함수와 테스트에서 사용하는 성능 지표는 다르다.
훈련에 사용되는 비용 함수는 최적화를 위해 미분이 가능해야 한다.
테스트에 사용되는 성능 지표는 최종 목표에 가능한 가까워야 한다.
ex. 릿지 회귀 - 훈련시킬 때는 위 비용함수를 활용하고, 성능 측정할 때는 MSE만을 활용한다.
로지스틱 회귀 - 훈련시킬 때는 로그 손실 비용 함수 활용하고, 성능 측정할 때는 정밀도/재현율 활용한다.
1.2 라쏘 회귀 Lasso
비용 함수에 규제항을 더하지만, 가중치 벡터의 l1 노름을 사용한다.

라쏘 회귀는 덜 중요한 특성의 가중치를 0으로 만들어 제거하려고 한다.
라쏘 회귀는 자동으로 특성 선택을 하고 희소 모델 sparse model 을 만든다.
즉 0이 아닌 특성의 가중치가 적은 모델을 만든다.
이제 라쏘 회귀 계산을 해보자.
라쏘 회귀를 계산하기 위해 선형 회귀와 마찬가지로 정규 방정식을 사용할 수도 있고, 경사 하강법을 사용할 수 있다.
(1) 라쏘 회귀 계수 추정 - 정규 방정식
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X,Y)
lasso_reg.predict([[1.5]])
(2) 라쏘 회귀 계수 추정 - 경사 하강법
라쏘는 특성 가중치 값 = 0 에서 미분 가능하지 않다.
특성 가중치 값 = 0 일때, 서브그레이디언트 벡터를 사용하여 경사하강법 진행한다.

사이킷런에서 SGDRegressor 를 사용하면 확률적 경사 하강법을 활용한다.
이때 penalty 파라미터를 l1으로 설정하면 라쏘 회귀를 구할 수 있다.
from sklearn.linear_model import SGDRegressor
#확률적 경사 하강법 활용 + 가중치 벡터에 대한 규제 적용
sgd_reg = SGDRegressor(penalty='l1')
sgd_reg.fit(X,Y.ravel())
sgd_reg.predict([[1.5]])
※ 라쏘회귀와 릿지회귀의 다른 점
- 라쏘 회귀
두 파라미터 중 0과 더 가까운 파라미터(세타2)를 0으로 빠르게 줄인다.
그 다음 축을 따라 진동하면서 전역 최적점(빨린 사각형)에 도달한다.
l1의 그레이디언트는 0에서 정의되지 않기 때문에, 약간의 진동 존재한다.
진동을 방지하기 위해서 점진적으로 학습률을 감소시켜야 한다.
알파 a값 증가하면 전역 최적점이 노란선을 따라 왼쪽으로 이동한다.
알파 a값이 커지면 파라미터 값들이 작아져야 하기 때문이다. - 릿지 회귀
파라미터가 전역 최적점에 가까워질수록 gradient가 작아진다.
따라서 자동으로 경사 하강법이 느려지고 수렴에 도움이 된다.
알파값을 증가시킬 수록 최적 파라미터(빨간 사각형)이 원점에 더 가까워진다.
하지만 완전히 0이 되지는 않는다.

1.3 엘라스틱넷
릿지 회귀와 라쏘 회귀를 절충한 모델이다.
혼합 정도는 혼합 비율 r로 조절한다.
이때 l1_ratio = 1 이면 Lasso 와 비슷한 모델이 생성되지만
l1_ratio = 0 이면 Ridge 와 비슷한 모델이 생성되지는 않는다.

import sklearn.linear_model import ElasticNet
# alpha = 엘라스틱넷 비용함수의 규제 정도 a
# l1_ratio = 엘라스틱넷 비용함수의 혼합 비율 r
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X,y)
elastic_net.predict([[1.5]])
※ 릿지, 라쏘, 엘라스틱넷 언제 사용해야 할까?
기본적으로 릿지를 사용한다.
다만, 쓰이는 특성이 몇 개 뿐이라고 의심되면 라쏘나 엘라스틱넷이 더 낫다.
그 이유는 불필요한 가중치를 0으로 만들어 주기 때문이다.
특성 수가 훈련 샘플 수보다 많으면 보통 라쏘는 문제를 일으킨다.
그 이유는 특성 수 > 샘플 수(n) 이면, 최대 n개의 특성을 선택하기 때문이다.
특성 몇 개가 강하게 연관되어 있을 때도 라쏘는 문제를 일으킨다.
그 이유는 연관된 특성 중 임의의 특성을 하나 선택하기 때문이다.
라쏘보다는 차라리 엘라스틱넷을 추천한다.
1.4 조기 종료
경사 하강법과 같은 반복적인 학습 알고리즘을 규제하는 색다른 방식은
검증 에러가 최솟값에 도달하면 바로 훈련을 중지시키는 것이다.
훈련 세트에 대해 성능 측정해보면 epoch 증가할수록 성능 증가한다.
하지만 검증 세트에 대해 성능 측정하면 성능이 증가하다 일정 epoch 이상부터는 성능이 감소한다.
확률적 경사 하강법이나 미니 배치 경사 하강법에서는 곡선이 매끄럽지 않아
최솟값에 도달했는 지 확인하기 어려울 수 있다.
이럴 경우, 검증 에러가 일정 시간 동안 최솟값보다 크면 성능이 더 나아지지 않는다고 보고
검증 에러 최솟값일 때의 모델 파라미터로 되돌린다.
위 설명한 조기 종료를 코드로 구현하면 다음과 같다.
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error
from sklearn.base import clone
poly_scaler = PipeLine([
('poly_features', PolynomialFeatures(degree=90, include_bias=False)),
('std_scaler', StandardScaler())
])
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.1)
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.fit_transform(X_val)
sgd_reg = SGDRegressor(max_iter=1, tol=np.infty, warm_start=True,
penalty=None, learning_rate='constant', eta0=0.0005)
minimum_val_error = float('inf')
best_epoch = None
best_model = None
for epoch in range(1000) :
sgd_reg.fit(X_train_poly_scaled, y_train_poly_scaled)
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
val_error = mean_squared_error(y_val, y_val_predict)
if val_error < minimum_val_error :
minimum_val_error = val_error
best_epoch = epoch
best_model = clone(sgd_reg)
SGDRegressor() 생성 시 warm_start, early_stopping, n_iter_no_change, tol 등을 설정할 수 있는데,
- warm_start
: True 이면 fit() 메서드를 호출할 때 처음부터 다시 시작하지 않고,
이전 모델의 파라미터에서부터 훈련이 이어진다. - early_stopping
: 조기 종료 설정 여부 - n_iter_no_change
: 해당 횟수만큼 연속적으로 성능 좋아지지 않으면 조기 종료 - tol
: 성능 개선 정도
이때, early_stopping 이 True 냐 False 냐에 따라 작동 방식이 다르다.
early_stopping = True 이면,
fit() 호출 시 내부적으로 X_train의 10%를 검증 데이터로 떼어서 검증 데이터 손실을 측정한다.
n_iter_no_change 횟수동안 tol 만큼의 개선이 없으면 조기 종료한다.
early_stopping = False 이면,
fit() 호출 시 X_train 전체 데이터의 손실을 측정한다.
n_iter_no_change 횟수동안 tol 만큼의 개선이 없으면 조기 종료한다.
'Machine Learning > 2. 지도 학습 알고리즘' 카테고리의 다른 글
| [분류] 선형판별분석(LDA) (0) | 2021.08.06 |
|---|---|
| [분류] 나이브 베이즈 (0) | 2021.08.06 |
| [회귀] 비선형 회귀 - 다항 회귀, 스플라인 회귀 (0) | 2021.08.06 |
| [회귀] 선형 회귀 가설 검정 : 회귀 진단 (0) | 2021.08.06 |
| [회귀] 선형 회귀 모델 해석 (0) | 2021.08.06 |




