[군집] 가우시안 혼합 모델

샘플마다 k개의 클러스터에서 랜덤하게 한 클러스터가 선택된다. j번째 클러스터를 선택할 확률은 클러스터의 가중치 ∮(j)로 정의된다. i번째 샘플을 위해 선택한 클러스터 인덱스는 z(i) 로 표시한다.
z(i) = j 이면, 즉 i번째 샘플이 j번째 클러스터에 할당되었다면 이 샘플의 위치 x(i)는 평균 m(j) 이고 공분산 행렬이 ∑(j) 인 가우시안 분포에서 랜덤하게 샘플링된다. x(i) ~ N(m(j) , ∑(j))와 같이 쓴다.

이 생성 과정을 그래프 모형으로 나타내면 다음과 같다.

<GMM의 그래프 모형 - 파라미터(사각형), 확률변수(원), 조건부 의존성(실선화살표) >

※ 가우시안 혼합 모델로 무엇을 하는가?

위 가정을 전제로 데이터 셋 X가 주어지면, 가중치 ∮와 전체 분포의 파라미터 m(1), ... , m(k) 와 ∑(1), ... , ∑(k) 까지를 추정한다.

다시 말해, 가우시안 혼합 모델을 훈련시킨다는 것은 가중치와 전체 분포 파라미터를 추정하는 것이다.

※ 그렇다면, 어떻게 가중치과 전체 분포의 파라미터를 추정할까?

GaussianMixture 클래스는 기댓값-최대화(EM) 알고리즘을 사용한다.

2. EM 알고리즘

클러스터 파라미터를 랜덤하게 초기화하고 수렴할 때까지 Expectation(기댓값) 와 Maximize(최대화) 두 과정을 반복한다.

2.1 과정

step1. E-step(기댓값 단계)

현재 클러스터 파라미터에 기반해 샘플이 각 클러스터에 속할 확률을 계산한다.

step2. M-Step(최대화 단계)

기능도 Likelihood 를 활용해, 각 샘플이 어떤 모델에서 생성되었을 때 가장 큰 확률을 갖는 지 확인하여, 모델의 파라미터를 추정하고 업데이트 한다.

위 두 과정을 간단한 수도 코드로 나타내면 다음과 같다.

2.2 수식 전개

위에서 살펴본 E-step 과 M-step 에서 진행되는 계산 수식을 살펴보면 다음과 같다.

3. GaussianMixture 클래스

3.1 모델 훈련

사이킷런에서 GaussianMixture는 매개 변수 n_components 를 통해 클러스터 갯수를 n_init 을 통해 반복 횟수를 지정할 수 있다.

훈련된 GaussianMixture 모델은 다양한 속성을 통해 각 클러스트의 위치, 크기, 모양, 방향, 상대적 가중치를 예측할 수 있다.

- weights_ : 클러스터 가중치

- means_ : 클러스터 별 가우시안 분포 파라미터 평균

- covariance_ : 클러스터 별 가우시안 분포 파라미터 공분산 행렬

- converged_ : 모델이 수렴했는 지 여부

from sklearn.mixture import GaussianMixture

gmm = GaussianMixture(n_components=3, n_init=10)
gmm.fit(X)
print(gmm.weights_)  #array([0.20965228, 0,400662, 0,39028152])
print(gmm.means_)
print(gmm.covariances_)

3.2 모델 예측

이 모델은 새로운 샘플을 가장 비슷한 클러스터에 손쉽게 할당할 수도 있다 (하드 군집). 또는 특정 클러스터에 속할 확률을 예측할 수 있다 (소프트 군집). 하드 군집을 위해서는 predict() 실행하고, 소프트 군집을 위해서는 predict_proba() 를 실행한다.

gmm.predict(X)
>> array([0, 1, 2, 0, 0, 1... ])

gmm.predict_proba(X)
>> array([[2.323444, 6.33455, 9.64556],
          [1.645552, 6.75334, 9.83234],
          ...
          [1.00034, 8.34422, 2.224465]])

3.3 새로운 샘플 생성

sample() 메서드를 통해 가우시안 혼합 모델은 생성 모델이다.

즉 이 모델에서 새로운 샘플을 만들 수 있다.

X_new, y_new = gmm.sample(6)

print(X_new)
>> array([[2.95400315, 2.636800992], [-1.16654575, 1.62792705], ... ]])

print(y_new)
>> array([0, 1, 2, 2, 2, 2])

3.4 확률 밀도 함수 (PDF)

score_samples() 메서드를 통해 주어진 위치에서 모델의 밀도 함수를 추정할 수 있다.

샘플이 주어진 그 위치의 확률 밀도 함수(PDF)의 로그를 예측한다.

score_samples() 점수가 높을 수록 밀도가 높은 것이다.

score_smaples() 결과의 지숫값을 구하면 샘플의 위치에서 PDF 값이다.

확률 밀도 함수(PDF) 란, 샘플 X를 알 때 모델 파라미터에 따라 해당 모델에서 생성되었을 가능성으로 0~1 사이의 값을 갖는다.

샘플 X가 모델에 포함될 확률과는 다르다!

샘플이 특정 지역(모델)에 포함될 확률을 예측하려면 PDF 를 적분해야 한다.

gmm.score_samples(X)
>> array([-2.060405, -3.566432, ... , -4.533432])

가우시안 혼합 모델의 클러스터 평균, 결정 경계(파선), 밀도 등고선을 보여준다.

3.5 모델 규제

특성이나 클러스터가 많거나 샘플이 적을 때는 EM이 최적의 솔루션으로 수렴하기 어렵다.

이런 작업의 어려움을 줄이려면 알고리즘이 학습할 파라미터 개수를 제한해야 한다.

이런 방법 중에 하나는 클러스터의 모양과 방향의 범위를 제한하는 것이다.

사이킷런에서 매개 변수 covariance_type 을 통해 제한할 수 있다.

spherial
모든 클러스터가 원형이다. 하지만 지름은 다를 수 있다. (즉 분산이 다르다.)

diag
클러스터는 크기에 상관없이 어떤 타원형도 가능하다. 하지만 타원의 축은 좌표축과 나란해야 한다.

tied
모든 클러스터가 동일한 타원 모양, 크기, 방향을 갖는다. 즉 모든 클러스터는 동일한 공분산 행렬을 공유한다.

full

클러스터 모양, 크기, 방향에 제약이 없다. 사이킷런의 기본갑이다.

4. 계산 복잡도

GausssianMixture 모델 훈련하는 계산 복잡도는

샘플 개수 m, 차원 개수 n, 클러스터 개수 k 와 공분산 행렬의 제약에 따라 결정된다.

covariance_type 이 spherial 이나 diag 인 경우, 데이터에 어떤 구조가 있다고 가정하므로 O(kmn) 이다.

covariance_type 이 tied 나 full 인 경우, O(kmn^2 + kn^2) 이다.

5. 클러스터 개수 선택하기

K-평균 처럼 GaussianMixture 알고리즘은 적절한 클러스터 개수를 지정해야 한다.

가우시안 혼합에서는 K-평균에서 사용한 이너셔나 실루엣 점수를 활용할 수 없다.

이런 지표들은 클러스터가 타원형이거나 크기가 다를 때 안정적이지 않기 때문이다.

대신, BIC 나 AIC 와 같은 이론적 정보 기준을 최소화하는 모델을 찾는다.

BIC와 AIC는 모두 학습할 파라미터가 많은(즉 클러스터가 많은) 모델에게 벌칙을 가하고

데이터에 잘 학습하는 모델에게 보상을 더한다. 이 둘은 종종 동일한 모델을 선택한다.

둘의 선택이 다를 경우, BIC가 선택한 모델이 AIC가 선택한 모델보다 간단한(파라미터가 적은) 경향이 있다.

하지만 데이터에 아주 잘 맞지는 않을 수 있다. (특히 대규모 데이터 셋에서 그렇다.)

print(gmm.bic(X))
print(gmm.aic(X))

여러 가지 클러스터 개수 K에 대한 AIC, BIC를 확인한 후, 정보 조건이 최소가 되는 지점의 K를 찾는다.

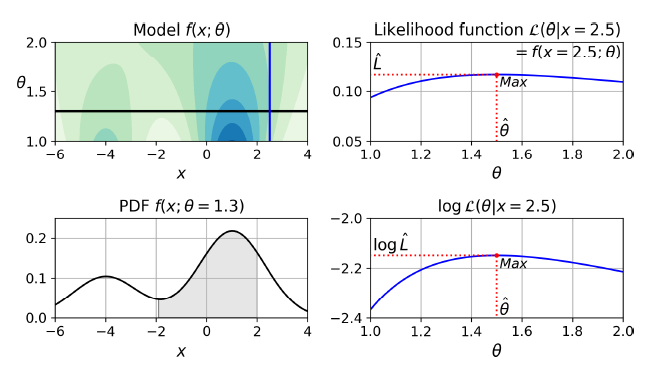
cf. 기능도 함수 (Likelihood)

확률 probablity 와 기능도 likelihood 는 종종 구별 없이 사용된다. 하지만 통계학에서 이 둘은 다른 의미를 갖는다.

확률 probablity는 파라미터 값을 알고 있을 때, X가 얼마나 그럴 듯한 지 설명한다.

기능도 Likelihood는 X를 알고 있을 때, 특정 파라미터가 얼마나 그럴 듯한 지 설명한다.

X의 확률 분포를 구하려면 ⊙를 지정해야 한다.

⊙를 1.3 으로 설정했을 때의 X 확률 분포를 알고자 한다면, Model f(X ; ⊙) 에서 ⊙ = 1.3 (수평선)으로 그어 왼쪽 아래 그래프 PDF f(X ; ⊙=1.3) 을 얻을 수 있다. 이제 X 값에 따른 확률 값을 알고자 한다면, PDF 를 적분하면 된다.

하지만 ⊙를 모른 채 X만 관측했다면, 관측한 X=2.5 (수직선)을 그어, 오른쪽 위 그래프에 나타난 기능도 함수를 얻을 수 있다.

확률 probablity 와 기능도 likelihood 는 종종 구별 없이 사용된다. 하지만 통계학에서 이 둘은 다른 의미를 갖는다.

확률 probablity는 파라미터 값을 알고 있을 때, X가 얼마나 그럴 듯한 지 설명한다.

기능도 Likelihood는 X를 알고 있을 때, 특정 파라미터가 얼마나 그럴 듯한 지 설명한다.

X의 확률 분포를 구하려면 ⊙를 지정해야 한다.

하지만 ⊙를 모른 채 X만 관측하여 최적의 ⊙를 알고자 한다면, 관측한 X=2.5 (수직선)을 그어 오른쪽 위 그래프에 나타난 기능도 함수를 얻을 수 있다. 데이터 셋 X가 주어졌을 때 모델 파라미터에 대해 가장 그럴듯한 ⊙값을 예측하기 위해서는 X에 대한 기능도 함수를 최대화하는 값을 구한다. Likelihood 최댓값은 Likelihood 함수의 로그에 대한 최대값과 동일하다. (Log Likelihood 를 구하는 것이 더 쉽다.)

기능도 함수를 최대로 하는 ⊙값을 추정하고 나면 AIC, BIC를 계산할 수 있게 된다.

6. 가우시안 혼합을 사용한 이상치 탐지

이상치 탐지는 보통과 많이 다른 샘플을 감지하는 작업이다.

이를 이상치라 부르고 보통 샘플을 정상치라고 부른다.

이상치 탐지는 다양하게 활용될 수 있다.

예를 들어, 부정 거래 감지, 제조 결함이 있는 제조 감지에 사용한다.

특히 실제로 다른 모델을 훈련시키기 전에 데이터 셋에서 이상치를 제거하는 데 사용 많이 한다.(모델 성능을 향상시킬 수 있다.)

가우시안 혼합 모델을 이상치 탐지에 사용하는 방법은 매우 간단하다.

밀도가 낮은 지역에 있는 모든 샘플을 이상치로 볼 수 있다.

이렇게 하려면 사용할 밀도 임계값을 정해야 한다.

예를 들어, 어떤 제조 회사가 결함 제품을 감지하고자, 결함을 판단하는 임계값을 결함 제품 비율 4%로 설정한다고 해보자.

만약 거짓양성이 너무 많다면 (정상인 제품을 결함 제품으로 판단) 임계값을 더 낮춘다.

반대로 거짓음성이 너무 많다면(결함 제품을 정산 제품으로 판단) 임계값을 높인다.

이렇게 정밀도/재현율 트레이드 오프를 고려하여 적절한 임계값을 정한다.

densities = gmm.score_samples(X)
density_threshold = np.percentile(densities, 4)
anomalies = X[densities < dnesity_threshold]

이와 비슷한 작업이 특이치 작업이다.

이 알고리즘은 이상치로 오염되지 않은 깨끗한 데이터 셋에서 훈련한다는 점이 이상치 탐지와 다르다.

Tip!

가우시안 혼합 모델은 이상치를 포함해 모든 데이터에 맞추려고 한다. 따라서 이상치가 너무 많으면 모델이 정상치를 바라보는 시각이 편향되고 일부 이상치를 정상으로 잘못 생각할 수 있다. 이런일이 일어나면 먼저 한 모델을 훈려한 뒤 가장 크게 벗어난 이상치를 제거한다. 그 다음 정제된 데이터 셋에서 모델을 다시 훈련한다.

또 다른 방법은 안정적인 공분산 추정 방법을 사용하는 것이다. (EllipticEnvelope 클래스 참고)

'Machine Learning > 3. 비지도 학습 알고리즘' 카테고리의 다른 글

[군집] 활용 - 개요 (0)	2023.08.19
[군집] 베이즈 가우시안 혼합 모델 (0)	2023.08.19
[군집] 스펙트럼 군집 (0)	2023.08.19
[군집] 유사도 전파 (0)	2023.08.19
[군집] BIRCH (0)	2023.08.19

'Machine Learning/3. 비지도 학습 알고리즘' Related Articles

My Data Story