My Data Story
[분류] 모델 평가 본문
◈ '분류' 목차 ◈
6. 분류 모델 평가
분류 모델의 다양한 평가 지표에 대해 이해하고, 잘 분류하기 위한 최적 임계값 선정하는 방법에 대해 알아보자.
1. 성능 측정
분류기 평가는 회귀 모델보다 훨씬 어렵다.
1.1 교차 검증을 통한 정확도 측정
분류모델의 평가는 일반적으로 교차 검증 진행한다.
cross_validate() 를 활용하면 교차 검증하는 데 걸리는 시간까지 추가 정보로 제공된다.
분류 모델에 대해 교차 검증 진행할 때 클래스 별 비율이 유지되도록 폴드를 만들도록 계층적 샘플링을 수행한다.
StratifiedKFold 통해서 계층적 샘플링하여 교차 검증 진행할 수 있다.
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import cross_val_score
skfolds = StratifiedKFold(n_splits=3, random_state=42)
cross_val_score(sgd_clf, X_train, y_train, cv=skfolds, scoring='accuracy')
Tip!
불균형한 데이터 셋을 다룰 때 (어떤 클래스가 다른 클래스보다 월등히 많은 경우), 정확도를 분류기 성능 측정 지표로 선호하지 않는다. 예를 들어, y값이 5가 아닌 데이터가 90%이라 할 때 모든 예측을 '5가 아님'이라 해도 90%의 정확도를 갖기 때문에 이는 정확도만을 갖고 모델의 예측 성능이 좋다고 말할 수 없다.
1.2 오차 행렬
분류기의 성능 평가를 위한 좋은 방법은 오차행렬 Confusion Matrix 를 조사하는 것이다.
오차 행렬 Confusion Matrix
| 구분 | 예측 | ||
| 실제 | 판단 | 음성 | 양성 |
| 음성 | TN | FP | |
| 양성 | FN | TP | |
(1) 정밀도 Precision
˙내가 예측한 양성 중 예측의 정확도 TP / (TP + FP)
˙이때 Precision 이 너무 높으면 False-Alarm 이 발생할 수 있다.
(2) 재현율 Recall
˙진짜 양성 중 내가 맞춘 양성 비율 TP / (TP + FN)
(3) F1 Score
˙F1Score는 정밀도와 재현율을 함께 사용하는 것이 일반적이라, 두 지표를 반영한 지표
˙F1 Score = 2 * {(정밀도 * 재현율) / (정밀도 + 재현율)}
˙F1 Score 가 높다고 항상 좋은 것은 아니다.
상황에 따라 정밀도가 중요할 수도, 재현율이 중요할 수 도 있다.
(4) 특이도 Specificity
˙ 실제 음성 중 내가 맞춘 진짜 음성의 비율 TN / (TN + FP)
(5) 거짓 양성 비율 FPR
˙내가 양성으로 예측한 샘플 중 음성 샘플의 비율 FP / (FP + TP)
˙FPR = '1- 특이도'
˙FPR은 정밀도와 반대되는 개념이다.
˙Confusion Matrix 에서 눈에 띄지 않지만 중요한 지표 중 하나이다.
※ 희귀 클래스 문제
많은 문제에서 분류해야 할 클래스 간에 불균형이 존재하는 경우가 대부분이다.
즉 한 클래스가 다른 클래스에 비해 훨씬 많이 발생하는 경우가 존재한다.
보통은 데이터 수가 상대적으로 작은 클래스가 관심의 대상이 되기 때문에 통상적으로 1로 지정하고
반대로 수가 많은 대상을 0으로 지정한다. 다시 말해, 일반적인 경우 1이 더 중요한 사건을 의미한다.
클래스를 쉽게 분리하기 어려운 경우, 가장 정확도가 높은 분류 모델은 모든 것을 무조건 0으로 분류하는 모델일 수 있다.
예를 들어 양성인 데이터가 5개이고 음성인 데이터가 95개 존재한다면, 무조건 음성이라고 분류해도 95%의 정확도를 얻는다.
이는 굉장히 잘못된 분류기임을 눈치챌 수 있다.
이럴 경우, 전반적인 정확도가 떨어지더라도 실제 1을 잘 골라내는 모델이 있다면 그 모델을 선택하는 것이 나을 수 있다.
문제에 따라 정밀도(내가 예측한 양성 중 진짜 양성의 비중) 와 재현율(진짜 양성 중 내가 맞춘 양성의 비중)을 잘 확인하여 모델을 평가한다.
1.3 오차행렬 python 구현
오차 행렬을 python으로 구현해보자.
오차 행렬을 만들려면 실제 타깃과 비교할 수 있는 예측값을 만들어야 한다.
훈련 데이터로 cross_val_predict()을 통해 예측값을 만든다.
cross_val_predict()는 cross_val_score() 처럼 k-겹 교차 검증을 수행하지만 평가 점수를 반환하지 않고,
각 테스트 폴드에서 얻은 예측을 반환한다.
Q. 왜 예측값 생성할 때, predict() 사용 안하고 cross_val_predict() 사용하나요?
훈련 데이터로 모델 훈련하고 훈련 데이터에 predict() 하여 예측하면 부정확한 값이 나올 수 있다.
따라서 cross_val_predicc() 을 통해 (k-1) 세트에 대해 훈련하고, 훈련때 보지 못한 나머지 세트에 대해 예측하는 교차 검증으로 예측값 생성한다.
※ 테스트 세트는 여기서 절대 사용하면 안된다! 테스트 세트는 모델 출시 전 가장 마지막에 사용한다!
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
confusion_matrix(y_train_5, y_train_pred)
분류 성능을 평가 지표에 대해 다음과 같이 구현할 수 있다.
from sklearn.metrics import precision_score, recall_score, f1_score
print(precision_score(y_train_5, y_train_pred))
print(recall_score(y_train_5, y_train_pred))
print(f1_score(y_train_5, y_train_pred))
1.3 ROC 곡선
앞서 살펴본 Confusion Matrix 에 있는 지표들은 사실 양성 클래스로 간주하는 Cut-Off 에 따라 결과가 달라진다.
우리는 Cut-Off 에 Independent 한 분류 성능 평가 지표가 필요하다. 이에 해당하는 지표 중 하나가 ROC 곡선이다.
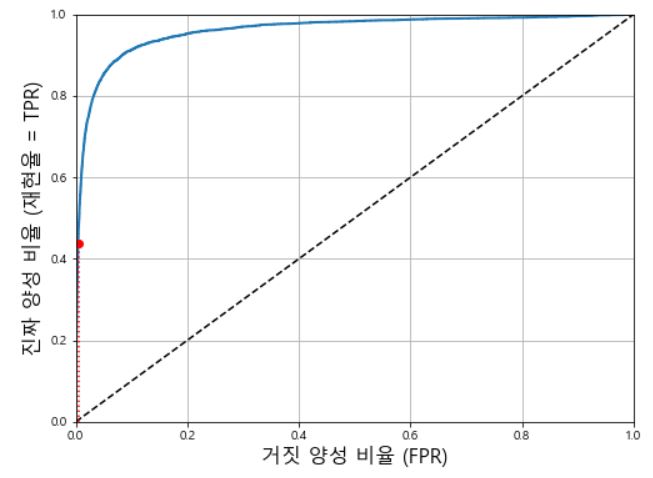
ROC 곡선은 거짓 양성 비율(FPR) 에 대한 진짜 양성 비율(TPR, 재현율)의 곡선이다.
ROC 곡선은 다음과 같이 그려진다.
step1. 각 데이터에 대한 P (양성 클래스일 확률) 값 기준으로 내림 차순 정렬한다.
step2. P에 대한 Cut-Off 별로 True Positive Rate 과 False Positive Rate을 계산한다.
step3. 각 Cut-Off 에서의 FPR값을 X축에 그리고 TPR 값을 Y축에 맵핑하여 그래프를 그린다.
ROC 곡선도 트레이드 오프 관계가 존재한다.
재현율이 증가할 수록 분류기가 만드는 거짓 양성이 늘어난다.
(거짓 양성 비율(FPR)은 1-특이도라, ROC 곡선은 재현율과 특이도 사이의 트레이드 오프 관계이기도 하다.)
ROC 곡선과 함께 나타나는 점선은 랜덤으로 예측했을 때의 결과를 의미한다.
극단적으로 효과적인 분류기는 ROC 곡선이 왼쪽 상단에 가까운 형태를 보일 것이다.
from sklearn.metrics import roc_curve
#ROC 곡선 그리기
fpr, tpr, threshold = roc_curve(y_train_5, y_scores)
def plot_roc_curve(fpr, tpr, label=None) :
plt.plot(fpr, tpr, line_width=2, label=None)
plt.plot([0,1],[0,1], 'k--') #가운데 대각 점선, 랜덤하게 예측할 경우에 대한 직선 함수
plot_roc_curve(fpr, tpr)
plt.show()
▶ ROC 곡선을 통한 RandomForest 모델과 SGD Classifier 모델간의 성능 비교
Tree 계열 모델은 모델 방정식이 존재하지 않아, decision_function 이 없다.
대신, Tree 계열 모델의 예측값 생성 시 예측의 확률을 얻는 predict_proba 방식을 활용한다.
from sklearn.ensemble import RandomForestClassifier
#RandomForest 모델 생성
forest_clf = RandomForestClassifier(random_state=42)
#RandomForest 활용하여 예측 확률 생성 (점수X)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
method='predict_proba')
#y_probas_forest에는 각 샘플마다 클래스 별 확률 존재
#양성 클래스에 대한 확률만을 점수로 사용한다.
y_score_forest = y_probas_forest[:,1]
#RandomForest 모델의 fpr, tpr 구하기
fpr_forest, tpr, threshold = roc_curve(y_train_5, y_score_forest)
#SGDClassifier 모델의 ROC 곡선 그리기
plt.plot(fpr, tpr, 'b:', label='SGD')
#RandomForest 모델의 ROC 곡선
plot_roc_curve(fpr_forest, tpr_forest, '랜덤포레스트')
plt.show()
1.4 AUC
ROC 곡선 자체로는 분류기 성능을 나타내는 값이 주어지진 않는다.
AUC는 ROC 곡선 아래쪽 면적을 계산한 값으로 AUC 값이 클수록 더 좋은 분류기라고 판단할 수 있는 지표가 된다.
최악의 분류기는 ROC 곡선이 가운데를 지나가는 직선인 경우이다.
이상적인 분류기는 AUC = 1 값을 갖고 랜덤 분류기 (최악 분류기)는 AUC=0.5 값을 갖을 것이다.
from sklearn.metrics import roc_auc_score
#ROC 곡선 아래 면적 AUC 측정하여 분류기를 비교할 수 있다.
roc_auc_score(y_train_5, y_scores)
AUC를 사용하면 전체적인 정확도도 높이면서 실무에서 중요한 1을 좀 더 정확히 분류해야 하는 트레이드 오프를 얼마나 잘 처리하는 지 평가할 수 있다. 하지만 희귀 케이스 문제에서 AUC가 높은 모델을 선택하면 모든 레코드를 0으로 분류할 수도 있음에 주의하자.
2. 적절한 임계값
2.1 precision_recall_curve() 활용
SGD Classifier 가 분류를 어떻게 결정하는 지 살펴보자.
step1
결정함수를 이용하여 각 샘플의 점수를 계산한다.
step2
이 점수가 결정 임계값보다 크면 양성 클래스에 할당하고, 작으면 음성 클래스에 할당한다.
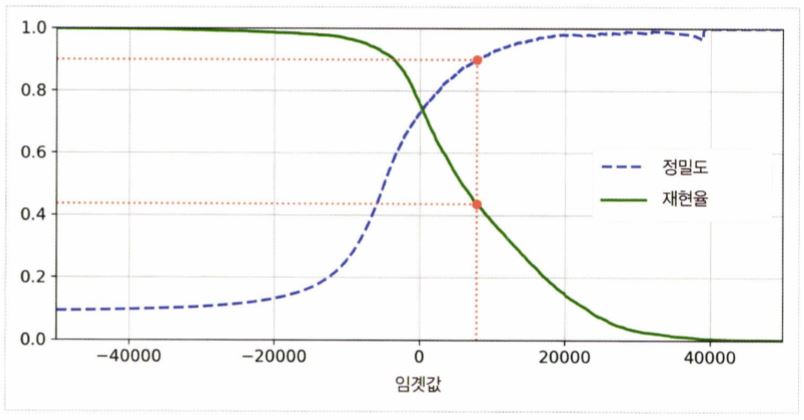
결정 임계값을 어디에 두느냐에 따라 정밀도와 재현율은 트레이드 오프 관계에 있다.
결정 임계값을 높이면 일반적으로 정밀도는 높아지고 재현율은 낮아진다.
사이킷런에서 결정 임계값을 직접 설정할 수 는 없지만, decision_function() 통해 각 샘플의 점수는 알 수 있다.
그 점수를 기반으로 임계값 생성할 수 있다. 결국 결정 임계값에 따라 각 샘플이 할당되는 클래스는 바뀔 수 있다.
아래 코드는 (1) 샘플의 점수 계산을 통해 (2) 직접 결정 임계값을 설정하여 (3) 클래스를 분류하는 과정에 대한 내용이다.
#step1. 각 샘플의 점수 계산
y_scores = sgd_clf.decision_function([some_digit])
#step2. 결정임계값 설정
threshold = 0
#step3. 각 샘플의 점수 > 결정임계값 이면, 양성 클래스로 할당
y_some_digit_pred = (y_score > threshold)
#결정임계값 변경하면, 각 샘플이 할당되는 클래스 바뀔 수 있다.
threshold2 = 8000
y_some_digit_pred2 = (y_score > threshold2)
적절한 결정 임계값을 안다면, 위 코드처럼 직접 결정 임계값을 설정하여 분류해도 좋다.
하지만 정밀도와 재현율은 트레이드 오프 관계에 있어 적절한 임계값을 정하기 어렵다.
이럴 때 사이킷런에서 precision_recall_curve() 를 활용해 정밀도-재현율 트레이드 오프 관계를 그래프로 나타내어
적절한 임계값 위치에 대한 인사이트를 얻을 수 있다.
step1
훈련 세트에 있는 모든 샘플의 점수를 구한다.
step2
가능한 모든 임계값에 따른 정밀도, 재현율 계산한다.
step3
matplot을 이용해 임계값의 함수로 정밀도와 재현율을 그려 비교한다.
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import precision_recall_curve
#step1. 각 샘플의 점수 계산
y_score = cross_val_predict(sgd_clf, X_train, y_train, cv=3, method='decision_function')
#step2. 임계값에 따른 정밀도, 재현율 계산
precision, recall, threshold = precision_recall_curve(y_train_5, y_scores)
#step3. 임계값에 따른 정밀도, 재현율 그리기
def plot_precision_recall_vs_threshold(precision, recall, threshold) :
plt.plot(threshold, precision[:-1], 'b--', label='정밀도')
plt.plot(threshold, recall[:-1], 'g--', labdel='재현율')
plot_precision_recall_vs_threshold(precision, recall, threshold)
plt.show()
#cf. 정밀도 90% 달성하는 것이 목표일 때, 임계값은?
threshold_90_precision = threshold[np.argmax(precision >= 90)]
2.2 PR 곡선 활용
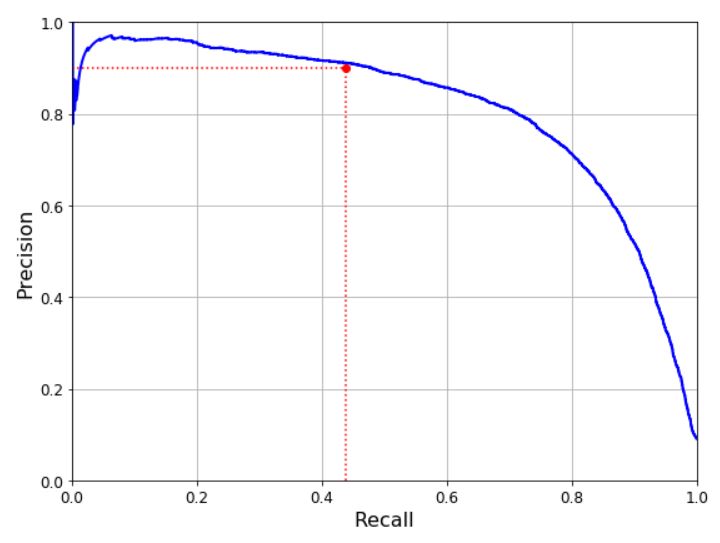
step1
재현율에 대한 정밀도 곡선을 그린다. (PR 곡선)
-> 좋은 분류기는 PR곡선이 오른쪽 위쪽으로 향한다.
step2
정밀도가 급격히 줄어들면서 기울기가 갑자기 변하는 지점을 임계값으로 선정한다.
-> 물론 이런 선정 기준도 분석 내용 및 목표에 따라 다르다.
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import average_precision_score
#step1. 정밀도, 재현율 계산
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method='decision_function')
precision, recall, threshold = precision_recall_curve(y_train_5, y_scores)
#step2. 재현율에 따른 정밀도 그리기
def plot_precision_recall(precision, recall) :
plt.plot(recall[:-1], precision[:-1], 'b--')
plot_precision_recall(precision, recall)
plt.show()
#cf. 곡선 아래쪽 면적 구하기 => 서로 다른 모델들끼리 비교하기 좋음
average_precision_score(y_train_5, y_scores)
▶ 그렇다면 ROC 곡선과 정밀도/재현율(PR) 곡선 중 어떤 것을 사용하는 것이 좋은가?
양성 클래스가 드물거나 거짓 음성보다 거짓 양성이 더 중요한 경우 PR 곡선 사용하고,
그렇지 않은 경우에는 ROC 곡선 사용한다.
2.3 리프트 곡선 활용
step1
클래스 1로 예측될 추정 확률 기준으로 내림차순 정렬한다. (추정 확률 높은 데이터 부터 차례로 나열)
step2
정렬된 데이터에 대해, 상위 십분위수(X축) 마다 재현율(Y축)을 나타내는 누적 이득 차트를 작성한다.

step3
상위 십분위수 마다 무작위로 선택했을 경우에 비해 얼마나 더 나은 지' 에 대한 리프트(이득)를 구한다.
리프트(이득)는 누적 이득 차트에서 각 십분위수에서 (Lift Curve값 - Baseline 값) / (Baseline 값) 의 비율이다.

리프트 곡선은 클래스 1로 분류하기 위한 cut-off 확률 값에 따른 결과의 변화를 한 눈에 볼 수 있게 해주어, 적합한 cut-off 확률을 결정하기 위한 중간 단계로 활용할 수 있다. 적절한 Lift를 선택하여 해당 Lift 일 때의 Cumulative Customer 비율(X축값) 확인한 후 해당 고객의 클래스 1 추정 확률을 cut-off 확률로 결정한다.
3. 에러 분석
가능성 높은 모델을 찾았을 때, 이 모델의 성능을 향상시키는 방법 중 하나가 만들어진 에러의 종류를 분석하는 것이다.
cross_val_predict()으로 예측을 만들고, confusion_matrix()로 오차 행렬 분석해본다.
잘못 분류한 케이스를 개선하기 위해서는 잘못 분류한 케이스의 훈련 데이터를 더 수집한 후 학습시키거나 분류기에 도움이 될 만한 특성을 더 찾아본다.
'Machine Learning > 2. 지도 학습 알고리즘' 카테고리의 다른 글
| [모델 알고리즘] 서포트 벡터 머신 - 선형 SVM 분류 (0) | 2021.08.09 |
|---|---|
| [분류] K 최근접 이웃(KNN) (0) | 2021.08.09 |
| [분류] 다중 레이블 분류, 다중 출력 분류 (0) | 2021.08.06 |
| [분류] 소프트맥스 회귀 (0) | 2021.08.06 |
| [분류] 로지스틱 회귀 (0) | 2021.08.06 |




